Целые

Целые являются основными объектами в вычислительной комбинаторике. В различных вычислительных теоретико-числовых исследованиях изучаются сами целые числа, но мы будем использовать их главным образом при подсчете и индексировании. В последнее время установлено, что полезны различные представления. В этой лекции обсудим общий класс позиционных представлений.

Мы будем рассматривать только неотрицательные целые. Кроме того, к любому представлению неотрицательных целых легко присоединить одиночный знаковый двоичный разряд.

Позиционные системы для представления целых чисел очень широко известны, поскольку они встречаются во многих разделах математики, начиная с "новой математики" и кончая углубленным курсом теории чисел. В системе счисления с основанием

каждое положительное целое число имеет единственное представление в виде конечной последовательности

(2.1)

в которой каждое

- целое, удовлетворяющее условию и . Нуль представляется последовательностью . называется основанием системы . Целое, соответствующее последовательности (2.1), имеет вид

что принято выражать следующим образом:

На протяжении истории использовались различные значения

. Например, древние вавилоняне использовали , а индейцы племени Майя — . Сегодня наиболее широко используется - десятичная система, которую мы унаследовали от арабов, и - двоичная система, которая лежит в основе современных вычислительных устройств. В действительности она применяется лишь на самом низком уровне аппаратного оборудования; в сложных вычислительных устройствах и базисных языках удобнее использовать или .

Единственность этого представления можно доказать методом от противного. Числа

и , очевидно, имеют единственное представление. Предположим, что представление не единственно, и пусть будет наименьшим целым числом, имеющим два различных представления:

Если

, то без потери общности предположим, что . Тогда, поскольку

и поскольку

, мы заключаем, что

(2.2)

что невозможно. Таким образом, мы должны иметь

. Аналогично, если , мы имели бы снова неравенство (2.2) и отсюда с необходимостью .
Следовательно, число



имеет два различных представления, что противоречит предположению, что - наименьшее из таких чисел.

Для доказательства того, что каждое положительное целое имеет представление по основанию , достаточно задать алгоритм, конструирующий (с необходимостью единственное) представление данного числа .

Алгоритм 1. Преобразование числа в его представление в системе счисления с основанием .

Он строит последовательность путем повторения деления на и записи остатков. Пусть на первом шаге при делении на остаток будет . Частное, полученное в результате первого шага, делим на , вновь полученное частное делим на и так далее. Полученная в результате такого процесса последовательность остатков и будет требуемым представлением по основанию .

Важным обобщением систем счисления с основанием являются смешанные системы счисления, в которых задается не единственное основание , а последовательность оснований и последовательность (2.2) соответствует целому

где теперь каждое удовлетворяет неравенству и , если - тот факт, что каждая такая последовательность соответствует единственному числу и каждое положительное целое число имеет единственное представление, следует из простого обобщения результатов для обычных систем счисления, которые являются частным случаем смешанных систем при .

Смешанные системы счисления могут вначале показаться странными, но в действительности в повседневной жизни они встречаются почти так же часто, как и десятичные.

Пример. Рассмотрим нашу систему измерения времени: секунды, минуты, часы, дни недели и годы. Это - в точности смешанная система с .

Представление целого в смешанной системе счисления осуществляется с помощью алгоритма 2, который является простым обобщением алгоритма 1. Вместо того, чтобы для получения в качестве делителя всегда использовалась , в алгоритме 2 используется .

Алгоритм 2. Преобразование числа в его представление в смешанной системе счисления

Последовательности

Бесконечная последовательность

формально определяется как функция

, областью определения которой является множество положительных целых чисел: . Во многих случаях индексирование последовательности более удобно начинать с нуля; тогда областью определения будет множество целых неотрицательных чисел. Аналогично определим конечную последовательность или список

как функцию, областью определения которой является множество

. Примером бесконечной последовательности являются простые числа

(2.3)

а перестановка

представляет собой пример конечной последовательности.

В комбинаторных алгоритмах часто приходится встречаться с представлениями конечных последовательностей (или начальных сегментов бесконечных последовательностей) и операциями над ними.

Различные способы представлений

Последовательное распределение. С вычислительной точки зрения простейшим представлением конечной последовательности является список ее членов, расположенных по порядку в последовательных ячейках памяти.

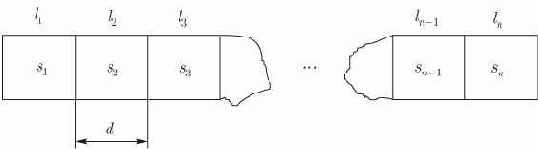
Рис. 2.1.

 

Последовательное распределение последовательности

для каждого элемента которой требуется ячеек

Так,

хранится, начиная с ячейки , хранится, начиная с ячейки , хранится, начиная с ячейки и так далее, где - число ячеек, требуемых для хранения одного элемента последовательности.

Описанное выше представление последовательности имеет ряд преимуществ. Во-первых, оно легко осуществимо и требует небольших расходов в смысле памяти. Кроме того, оно полезно и потому, что существует простое соотношение между

и адресом ячейки, в которой хранится :

Это соотношение позволяет организовать прямой доступ к любому элементу последовательности. Наконец, последовательное представление имеет достаточно широкий диапазон и включает в себя в качестве специального случая представление многомерных массивов.

Например, чтобы представить массив размером

(2.4)

будем рассматривать его как последовательность

, в которой каждое в свою очередь является последовательностью из элементов -й строки нашей матрицы. Таким образом, число ячеек, требуемых для записи элемента (будем обозначать это число символом ), равно , где - число ячеек, требуемых для записи элемента . Поскольку последовательность начинается в ячейке

ячейка для

будет иметь следующий адрес:

Это представление известно как построчная запись матрицы; постолбцовая запись получается, если (2.4) рассматривать как последовательность

в которой каждое в свою очередь является последовательностью из элементов -го столбца матрицы.

Последовательное распределение, наряду с преимуществами, имеет значительные недостатки. Например, такое представление становится неудобным, если требуется изменить последовательность путем включения новых и исключения имеющихся там элементов. Включение между

и нового элемента требует сдвига вправо на одну позицию; аналогично, исключение требует сдвига тех же элементов на одну позицию влево. С точки зрения времени обработки, такое передвижение элементов может оказаться дорогостоящим, и в случае динамических последовательностей лучше использовать технику связного распределения, рассматриваемую в следующей лекции.

Характеристические векторы. Важной разновидностью последовательного распределения является случай, когда такому представлению подвергается последовательность некоторой основной последовательности

В этом случае можно представить последовательность более удобно, используя характеристический вектор - последовательность из нулей и единиц, где -й разряд равен единице, если принадлежит рассматриваемой последовательности, и нулю в противном случае.

Например, характеристический вектор начального сегмента последовательности (2.3)

характеристический вектор для простых чисел:

Здесь основной последовательностью является последовательность целых положительных чисел. В ЭВМ с 32-разрядными словами для запоминания простых чисел, меньших

, потребуется слов. Замечая далее, что для число не простое, можно сэкономить половину этого поля, выписывая разряды только для чисел видов , и запоминая, что простое число 2 отсутствует. Таким образом, простые числа, меньшие чем , можно записать только 15625 словами. Поскольку число простых чисел, меньших , равно 78498, последовательное представление, описанное ранее, потребовало бы поля в пять раз меньшего размера.

Характеристические векторы полезны в ряде случаев. Их полезность вытекает из их компактности, существования простого фиксированного соотношения между

и адресом -го разряда и возможности при таком представлении очень легко исключать элементы.

Главное неудобство характеристических векторов состоит в том, что они не экономичны. Исключение составляют "плотные" последовательности последовательностей

. Кроме того, их трудно использовать, если не существует простого соотношения между и .Если такое соотношение сложное, то использование характеристических векторов может быть очень не экономичным в смысле времени обработки. Если последовательности недостаточно плотные, то значительным может оказаться объем памяти. В случае простых чисел между и имеется простое соотношение: (или , если использовать только нечетные числа). Теорема о простых числах утверждает, что число простых чисел, меньших , приблизительно равно ; таким образом, простые числа относительно плотно распределены в множестве целых чисел.

в качестве основных объектов допускает

Большинство вычислительных устройств в качестве основных объектов допускает только двоичные наборы, целые и символы, поэтому, прежде чем работать с более сложными объектами, их необходимо представить двоичными наборами, целыми или символами. Например, числа с плавающей запятой кодируются целыми - мантиссой и порядком этого числа, но такое кодирование обычно незаметно для пользователя. В противоположность этому, рассмотренные во второй и третьей лекции способы кодирования объектов (множества, последовательности, деревья) всегда адресованы пользователю.
Любой заданный класс объектов может иметь несколько возможных представлений, и выбор наилучшего из них решающим образом зависит от того, каким образом объект будет использован, а также от типа производимых над ним операций. Поэтому рассмотрим не только свойства самих представлений, но также и некоторые приложения.

Программы

Программа 1. Создание списка.

// Алгоритм реализован на языке программирования Turbo-C++. #include <stdio.h> #include <conio.h> #include <dos.h>

struct List{int i; List*next; }; List*head=NULL;

void Hed(int i) {if(head==NULL){head=new List; head->i=1; head->next=NULL; }else { struct List*p,*p1; p=head; while(p->next!=NULL) p=p->next;

p1=new List; p1->i=i; p1->next=NULL; p->next=p1; } }

int s=0;

void Print(List*p) {cprintf(" %d",p->i); if(p->next!=NULL)Print(p->next); }

void delist() {List*p; while(head!=NULL) {p=head; head=head->next; delete(p); } } void Vstavka(int i1,int c) {List*p=head,*p1; while(p->i!=i1) p=p->next; p1=new List; p1->i=c; p1->next=p->next; p->next=p1; }

void main() { clrscr(); for(int i=1;i<=10;i++) Hed(i); textcolor(12); Print(head); textcolor(1); Vstavka(10,11); printf("\n"); Print(head); textcolor(11); Vstavka(3,12); printf("\n"); Print(head); textcolor(14); Vstavka(5,13); printf("\n"); Print(head); delist(); getch(); }

Программа 2. Создание стека и работа со стеком.

//Работа со стеком // Алгоритм реализован на языке программирования Turbo-C++. #include <stdio.h> #include <dos.h> #include <iostream.h> #include <PROCESS.H> #include <STDLIB.H> #include <conio.H> #define max_size 200 // char s[max_size]; //компоненты стека int s[max_size]; int next=0; // позиция стека int Empty() { return next==0; } int Full() { return next==max_size; } void Push() { if (next==max_size) { cout <<"Ошибка: стек полон"<<endl;}

else { next++;cout <<"Добавлен"<<endl; cout <<"Что поместить в стек?"<<endl; cin <<s[next-1]; } } void OUTst() {int i=0; if (next==0) { cout <<"Cтек пуст"<<endl;}

else { for(i=0;i <next;i++) cout <<s[i] <<"" <<endl; } } void Clear() { next=0; } Poz() { return next; } void Del() { int a; if (next==0) cout <<"Ошибка: стек пуст" <<endl; else {next--;cout <<"Удален" <<endl;} } void menu(){ cout <<"0: распечатать стек" <<endl; cout <<"1: добавить в стек" <<endl; cout <<"2: удалить из стека" <<endl; cout <<"3: узнать номер позиции в стеке" <<endl; cout <<"4: узнать, пуст ли стек" <<endl; cout <<"5: узнать, полон ли стек" <<endl; cout <<"6: очистить стек" <<endl; cout <<"7: выход" <<endl; } main() { char c; clrscr(); textcolor(11); do { menu(); cin"c; clrscr(); switch (c) { case "0":OUTst();getch();break; case "1":Push();break; case "2":Del();getch();break; case "3":cout <<"Hомер" <<Poz() <<endl;getch();break; case "4":if (Empty()==1) cout <<"Пуст" <<endl; else cout <<"Hе пуст" <<endl;getch();break; case '5':if (Full()==1)cout <<"Полн" <<endl; else cout <<"Hе полон" <<endl;getch();break; case '6':Clear();cout <<"Стек очищен" <<endl;getch();break; case '7':exit(1); } delay(200); } while (c!=7); return 0; }

Разновидности связанных списков

Тривиальной модификацией связанного списка, изображенного на рис 3.2, будет следующее несколько более гибкое представление последовательности: если

указывает на , как показано на рис.3.5, то мы имеем так называемый циклический список. Такая форма списка дает возможность достигнуть любой элемент из любого другого элемента последовательности. Включение и исключение элементов здесь осуществляется так же, как и в нециклических списках, в то время как сцепление и разбиение реализуются несколько более сложно.

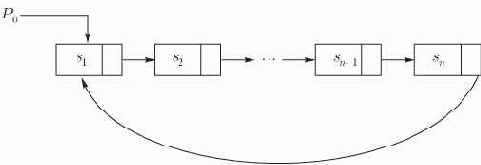
Рис. 3.5.  Циклический список

Еще большая гибкость достигается, если использовать дважды связанный список, когда каждый элемент

последовательности вместо одного имеет два связанных с ним указателя. Как показано на рис. 3.6, они указывают на элементы и . В таком списке для любого элемента имеется мгновенный прямой доступ к предыдущему и последующему элементам, в связи с чем облегчаются такие операции, как включение нового элемента перед и исключение элемента

без предварительного знания его предшественника. Если есть необходимость, дважды связанный список очевидным образом можно сделать циклическим.

Рис. 3.6.  Дважды связанный список

Стеки и очередь

В комбинаторных алгоритмах особую важность представляют две структуры данных, основанные на динамических последовательностях, т.е. последовательностях, которые изменяются вследствие включения новых и исключения имеющихся элементов. В обоих случаях операции включения и исключения, которым подвергается последовательность, имеют ограниченный вид: они производятся только в концах последовательности. Стек есть последовательность, у которой все включения и исключения происходят только в ее правом конце, называемом вершиной стека (соответственно, левый конец последовательности называется основанием). Таким образом, элементы включаются в стек и исключаются из него в соответствии с правилом "Первым пришел - последним ушел". Очередь - это последовательность, в которой все включения производятся на правом конце списка (в конце очереди), в то время как все исключения производятся на левом конце (в начале очереди). В противоположность стеку очередь оперирует в режиме "Первым пришел - первым ушел".

Стеки и очереди имеют важное значение. Для выполнения какой-либо определенной задачи может потребоваться выполнение ряда подзадач. Каждая подзадача может также привести к другим требующим выполнения подзадачам. И стеки, и очереди являются механизмом, посредством которого запоминаются подзадачи, подлежащие выполнению, а также порядок, в котором они должны быть выполнены. В некоторых случаях порядок таков: "Первым пришел - последним ушел"; тогда удобно использовать стеки. Если порядок подчиняется правилу "Первым пришел - первым ушел", то подходящим инструментом являются очереди.

Связанное распределение

В лекции 11 даны примеры и программные реализации списков, стеков и очередей. Неудобство включения и исключения элементов при последовательном распределении происходит из-за того, что порядок следования элементов задается неявно требованием, чтобы смежные элементы последовательности находились в смежных ячейках памяти. В результате многие элементы последовательности во время включения или исключения должны передвигаться. Если это требование опущено, то можно выполнить операции включения и исключения без того, чтобы передвигать элементы последовательности. При связанном распределении последовательности (связанном списке) каждому

поставлен в соответствии указатель (ссылка)

, отмечающий ячейку, в которой записаны и . Существует также указатель , который указывает начальную ячейку последовательности, то есть ячейку с символами и . Все сказанное выше проиллюстрировано на рис. 3.1.

Рис. 3.1. 

Здесь каждый узел состоит из двух полей. Под узлом понимается одно или несколько последовательных слов в памяти машины, которые выступают как единое целое и разделены на части, именуемые полями. В поле

размещен сам элемент последовательности, а в поле - указатель на следующий за ним элемент.

Linked list - список с использованием указателей: список, в котором каждый элемент содержит указатель на следующий элемент или два указателя - на следующий и предыдущий. Поскольку для

следующего элемента не существует, будем использовать обозначение , где - пустой , или нулевой указатель . Так как точные значения для программиста не существенны, то в более общем виде связанное представление, показанное на рис. 3.1, можно изобразить так, как показано на рис.3.2.

Рис. 3.2.  Другой, более употребительный, способ представления списка

Связанное представление последовательностей облегчает операции включения элемента после некоторого

и исключения элемента , если ячейка для известна. Для этого необходимо лишь изменить значения некоторых указателей. Например, чтобы исключить элемент из последовательности, изображенной на рис. 3.2, необходимо только положить

после такой операции элемента в последовательности больше не будет (рис.3.3). Чтобы в последовательность, изображенную на рис. 3.2, включить новый элемент , необходимо только воспроизвести новый элемент в некоторой ячейке с и и присвоить .Это изображено на рис.3.4.


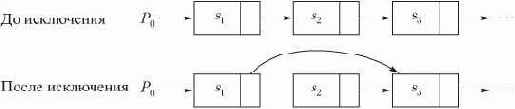
Рис. 3.3.  Исключение элемента из связанного списка


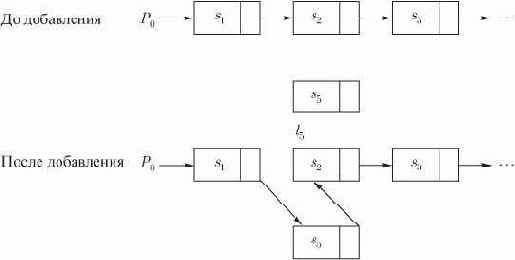
Рис. 3.4.  Включение элемента в связанный список

Использование связанного представления предполагает существование некоторого механизма, который по мере надобности поставляет новые ячейки и собирает старые ячейки, когда они освобождаются, но эта проблема выходит за рамки нашего курса.

Будем предполагать, с целью использования в различных алгоритмах, существование операции порождения ячейки get_cell; если эта операция присутствует в правой части оператора присваивания, то она дает адрес (место) новой неиспользованной ячейки памяти. Таким образом, чтобы добавить элемент , как показано на рис. 3.4 нужно фактически использовать оператор get_cell для того чтобы найти значение . Проблему сбора ненужных ячеек памяти будем полностью игнорировать, предполагая лишь, что их каким-то образом собирают для последующего использования; такой процесс носит название сбора мусора.

Недостаток при связанном распределении - приходится тратить память на указатели . В приложениях при выборе последовательного или связанного представления нужно сначала проанализировать типы операций, которые будут выполняться над последовательностью. Если операции производятся преимущественно над случайными элементами, осуществляют поиск специфических элементов или производят упорядочение элементов, то обычно лучше применять последовательное распределение. Связанное распределение предпочтительнее, если в значительной степени используются операции включения и(или) исключения элементов, а также сцепления и (или) разбиения последовательностей.

Модифицированный список

Задача 1. Создать список, элементами которого являются числа: 1 2 3 4 5 6 7 8 9. Вывести список на экран терминала. Включить в связанный список элемент 2005 после каждого элемента, который делится на 3. Модифицированный список вывести на экран терминала.
Задача 2. Очередью с приоритетом называется линейный список, который оперирует в режиме "первым включается - с высшим приоритетом исключается"; иными словами, каждому элементу очереди сопоставлено некоторое число - приоритет. Включения производятся в конец очереди, а исключения - в любом месте очереди, поскольку исключаемый элемент - это всегда элемент с высшим приоритетом. Нужно описать алгоритм (и его реализацию) включения и исключения для очередей с приоритетом.

Деревья

Конечное корневое дерево

формально определяется как непустое множество упорядоченных узлов, таких, что существует один выделенный узел, называемый корнем дерева, а оставшиеся узлы разбиты на

поддеревьев

. Будем рассматривать только корневые деревья. Узлы, не имеющие поддеревьев, называются листьями; остальные узлы называются внутренними узлами.

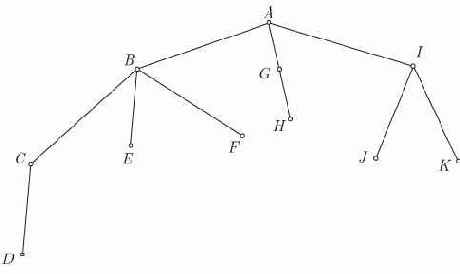
Рис. 4.1.

 

Дерево с 11 узлами, помеченными буквами от

до . Узлы с метками являются листьями; другие узлы внутренние. Узел с меткой - корень

В первой лекции уже было использовано дерево - при изучении необходимого числа взвешиваний в задаче о фальшивой монете с

монетами. Так "рано" деревья появились в тексте не случайно, поскольку понятие дерева используется в различных важных аспектах данного курса. Посредством деревьев изображаются иерархические организации, поэтому они являются наиболее важными нелинейными структурами в комбинаторных алгоритмах.

В описании соотношений между узлами дерева используем терминологию, принятую в генеалогических деревьях. Так, говорят, что в дереве или поддереве все узлы являются потомками его корня, и наоборот, корень есть предок всех своих потомков. Корень именуют отцом корней его поддеревьев, которые в свою очередь будут сыновьями корня. Например, на рис. 4.1 узел

является отцом узлов и ; - сыновья , а - братья.

Все рассматриваемые нами деревья будут упорядочены, то есть для них будет важен относительный порядок поддеревьев каждого узла. Таким образом, деревья считаются различными.

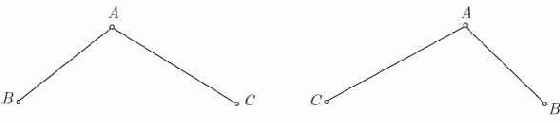
Рис. 4.2.  Различные деревья

Определим лес как упорядоченное множество деревьев; в связи с этим можно перефразировать определение дерева: дерево есть непустое множество узлов, такое, что существует один выделенный узел, называемый корнем дерева, а оставшиеся узлы образуют лес с

поддеревьями корня. Важной разновидностью корневых деревьев является класс бинарных деревьев. Бинарное дерево

либо пустое, либо состоит из выделенного узла, называемого корнем, и двух бинарных поддеревьев: левого и правого .
Бинарные деревья не являются подмножеством множества деревьев, они полностью отличаются по своей структуре, поскольку два следующих рисунка не изображают одно и то же бинарное дерево.


Рис. 4.3.  Различные бинарные деревья

Как деревья, однако, они не отличаются от дерева, изображенного на рис. 4.4.


Рис. 4.4.  Не бинарное дерево

Различие между деревом и бинарным деревом состоит в том, что дерево не может быть пустым, а каждый узел дерева может иметь произвольное число поддеревьев; в то же время, бинарное дерево может быть пустым. Каждая из вершин бинарного дерева может иметь 0, 1 или 2 поддерева, и существует различие между левым и правым поддеревьями.

Длина путей

Деревья можно использовать не только как способ представления структуры данных, но также как средство для анализа поведения определенных алгоритмов. В связи с этим возникает потребность в количественных измерениях различных характеристик деревьев и, в частности, бинарных деревьев.

Наиболее важные количественные характеристики деревьев связаны с уровнями узлов. Уровень

определяется рекурсивно и считается равным нулю, если корень ; в противном случае уровень определяется как . Понятие уровня дает возможность определить высоту дерева :

Другими словами, высота дерева есть максимальное число ребер, образующих путь от корня к листу дерева.

Представления

Почти все машинные представления деревьев основаны на связанных распределениях. Каждый узел состоит из поля

и нескольких полей для указателей. Например, представление, которое будет удобным для изложения множества и мультимножества, для каждого узла имеет единственное поле для указателя , указывающего на отца данного узла. При этом приведенное на рис. 4.1 дерево будет выглядеть так, как показано на рис. 4.6.

Такое представление полезно, если необходимо подниматься по дереву от потомков к предкам. Такая операция встречается довольно редко. Чаще требуется опуститься по дереву от предков к потомкам.

Представление дерева (или леса) с использованием указателей, ведущих от предков к потомкам, довольно сложно, поскольку узел, имея не более чем одного отца, может в то же время иметь произвольно много сыновей. Другими словами, при таком представлении узлы должны различаться по размеру, что является определенным неудобством. Один из путей обхода этой трудности состоит в том, чтобы определить соответствие между деревьями и бинарными деревьями, поскольку бинарные деревья легко представить узлами фиксированного размера.

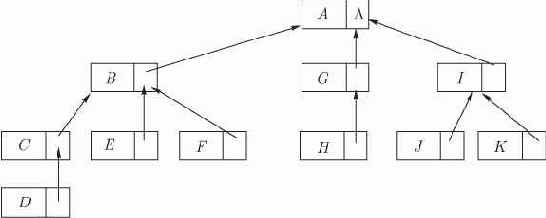
Рис. 4.5.  Дерево из рис. 4.1, представленное с помощью узлов с полем и указателем

Каждый узел в этом случае имеет три поля:

, указатель местоположения корня левого поддерева, , содержимое узла, и , указатель местоположения корня правого поддерева. Все сказанное выше проиллюстрировано на рис. 4.6.

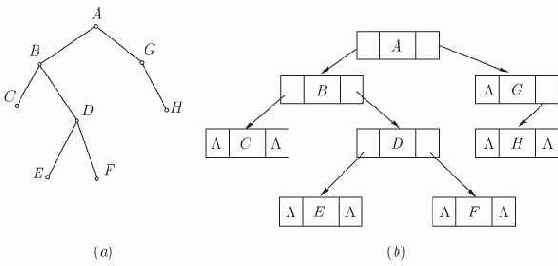
Рис. 4.6.  Бинарное дерево и его представление с помощью узлов с тремя полями , ,

Можно представлять деревья как бинарные, используя узлы фиксированного размера, представляя каждый узел леса в виде узла, состоящего из полей

, , . При этом

предназначается для указания самого левого сына данного узла, а поле

- для указания следующего брата данного узла.

Программa

Программа 1. Обход бинарного дерева в глубину

//Обход ориентированных графов - поиск в глубину - //обобщение обхода дерева в прямом порядке #include <stdio.h> #include <string.h> #include <conio.h> #include <stdlib.h>

int matr_sm[50][50]; int mark[50]; int n;

void vvod () {int v1,v2; printf("Введите кол-во вершин в графе: "); do { scanf("%d",&n); if (n>51) printf("Ошибка!! Введите кол-во вершин в графе: "); } while (n>51);

for (int i=0;i <50;i++) for (int j=0;j <50;j++) matr_sm[i][j]=0;

printf("\nВведите связанные вершины : \n"); do { scanf("%d ",&v1); if (v1>n) //исходящая вершина { printf("ОШИБКА ВВОДА !!!!!!!!!"); abort(); } if (v1==0){break;} // конец ввода scanf(" %d ",&v2); if (v2>n) // входящая вершина { printf("ОШИБКА ВВОДА !!!!!!!!!"); abort(); } if (v2==0){break;} //конец ввода matr_sm[v2-1][v1-1]=1; } while(1); }

void vivod() { for (int j=0;j <n;j++) { for (int i=0;i<n;i++) printf("%d ",matr_sm[j][i]); printf("\n"); } }

void dfs(int v) { int w; mark[v]=1; //посетили printf("%i ",v+1); //и выдали на экран for (w=0;w<n;w++) if (matr_sm[v][w]==1); else if (mark[w]==0) dfs(w); }

void main() { clrscr(); vvod(); // printf("\n"); printf("МАТРИЦА СМЕЖНОСТИ\n"); // vivod();

printf("\n РЕЗУЛЬТАТ ПОИСКА В ГЛУБИНУ \n"); for (int v=0;v<50;v++) mark[v]=0; for (v=0;v<n;v++) //если вершина не посещалась, то посетить if (mark[v]==0) dfs(v);

getch(); }

Прохождения

Во многих приложениях необходимо пройти лес, заходя в узлы, то есть обрабатывая их некоторым систематическим образом. Посещение каждого узла может быть связано с простой операцией, такой как печать содержимого, или со сложной, такой как вычисление функции. Будем предполагать, что при посещении узла структура леса не меняется. Рассмотрим четыре основных способа прохождения леса: в глубину, снизу вверх, в горизонтальном порядке и для бинарных деревьев - в симметричном порядке.

При прохождении в глубину, известном также как прохождение в прямом порядке, узлы леса проходятся в соответствии со следующей рекурсивной процедурой:

Посетить корень первого дерева.пройти в глубину поддерева первого дерева (если оно есть).Пройти в глубину оставшиеся деревья, если они есть.

Например, для леса, показанного на рис. 4.7, узлы будут проходиться в следующем порядке:

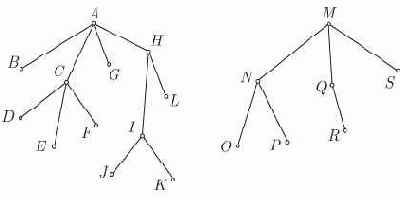
Рис. 4.7.  Лес

Название "в глубину" отражает тот факт, что после посещения некоторого узла мы продолжаем прохождение в глубь дерева всякий раз, когда это возможно. Такой порядок особенно полезен в процедурах поиска.

Для бинарных деревьев эта процедура упрощается и выглядит следующим образом.

Посетить корень.Пройти в глубину левое поддеревоПройти в глубину правое поддерево.

Прохождение снизу вверх, известное также как обратный порядок или концевой порядок, осуществляется согласно следующей рекурсивной процедуре:

Пройти снизу вверх поддеревья первого дерева, если они есть.Посетить корень первого дерева.Пройти снизу вверх оставшиеся деревья, если они есть.

Название "снизу вверх" связано с тем, что в момент посещения произвольного узла его потомки оказываются уже пройденными. Такой порядок прохождения полезен, в частности, потому, что он позволяет вычислять рекурсивно определенные функции на лесах. При этом порядке прохождения узлы леса, показанного на рис. 4.7, проходятся в такой последовательности:

. Рекурсивная процедура прохождения снизу вверх применительно к бинарным деревьям имеет следующий вид:

Пройти снизу вверх левое дерево.Пройти снизу вверх правое дерево.Посетить корень.

Симметричный порядок для бинарных деревьев определяется рекурсивно следующим образом:

Пройти в симметричном порядке левое поддерево.Посетить корень.Пройти в симметричном порядке правое поддерево.

Такой способ прохождения известен также как лексикографический порядок или внутренний порядок. Заметим, что прохождение леса снизу вверх эквивалентно прохождению в симметричном порядке бинарного дерева, соответствующего этому лесу (при естественном соответствии).

Сравнивая рекурсивные процедуры прохождения бинарных деревьев в глубину, снизу вверх и в симметричном порядке, можно обнаружить их значительное сходство:

прохождение в глубинусимметричный порядокпрохождение снизу вверх

посетить корень	левое поддерево	левое поддерево
левое поддерево	посетить корень	правое поддерево
правое поддерево	правое поддерево	посетить корень

Это сходство позволяет построить общий нерекурсивный алгоритм, который может быть применен к каждому из этих порядков прохождения бинарных деревьев.

Горизонтальный порядок прохождения. При таком способе узлы леса проходятся слева направо, уровень за уровнем от корня вниз. Таким образом, в соответствии с этой процедурой узлы леса, показанного на рис.4.7, будут проходиться в следующем порядке: . Такое прохождение дерева полезно в определенных алгоритмах на графах.

Построить алгоритм обхода

Задача 1. Построить алгоритм обхода бинарного дерева (см. рис. 4.6,(а)) в глубину.

Число сочетаний

Рассмотрим подмножества множества, состоящего из пяти элементов, и подсчитаем их число. При этом записывать подмножества будем не с помощью букв, как обычно, а в виде последовательностей длиной пять, составленных из нулей и единиц. Каждая из единиц указывает на наличие в подмножестве соответствующего элемента. Например, подмножества, содержащие один элемент, будут изображаться следующими последовательностями: 10000, 01000, 00100, 00010, 00001. Пустое подмножество

будет соответствовать последовательности 00000. Подмножества, содержащие по два элемента из пяти, запишутся с помощью следующих последовательностей: 11000, 10100, 10010, 10001, 01100. 01010, 01001, 00110, 00101, 00011. Всего их .

Вообще, число сочетаний из

элементов по равно числу всевозможных последовательностей из единиц и нулей.

Деревья и перестановки из n элементов

С помощью леса можно представить перестановки из

элементов множества (множество мы определяем так: множество - это неупорядоченная совокупность различных объектов или структура данных, используемая для представления множества). Подсчитаем, сколько можно получить перестановок. Для такой лес изображен на рис. 5.1.

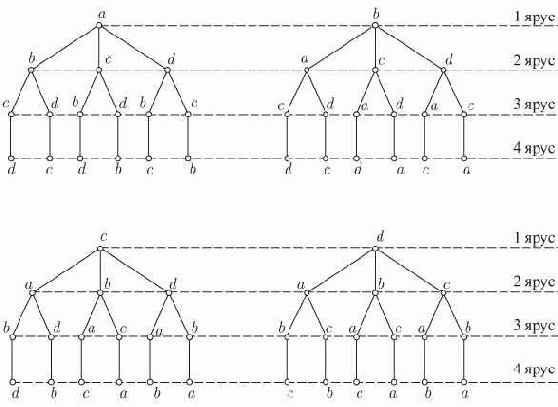
Рис. 5.1.  Всевозможные перестановки прочитываются по этой схеме от корневой до висячей вершины соответствующего дерева. Ярус показывает номер места, на котором расположен элемент. Число висячих вершин леса равно числу перестановок

Комбинаторные задачи теории информации

Информация - сведения, неизвестные до их получения, или данные, или значения, приписанные данным.

Теория информации - математическая дисциплина, изучающая количественные свойства информации.

Задачу, похожую на только что решенную, приходится решать в теории информации. Предположим, что сообщение передается с помощью сигналов нескольких типов. Длительность передачи сигнала первого типа равна

, второго типа - -го типа - единиц времени.

Задача 6. Сколько различных сообщений можно передать с помощью этих сигналов за

единиц времени? При этом учитываются лишь "максимальные" сообщения, то есть сообщения, к которым нельзя присоединить ни одного сигнала, не выйдя за рамки отведенного для передачи времени.

Обозначим число сообщений, которые можно передать за время

через . Рассуждая точно так же, как и в задаче о марках, получаем, что удовлетворяет соотношению

(5.8)

При этом снова , если и

Разные статистики

Задачи о раскладке предметов по ящикам весьма важны для статистической физики. Эта наука изучает, как распределяются по своим свойствам физические частицы; например, какая часть молекул данного газа имеет при данной температуре ту или иную скорость. При этом множество всех возможных состояний распределяют на большое число

маленьких ячеек (фазовых состояний), так что каждая из частиц попадет в одну из ячеек.

Вопрос о том, какой статистике подчиняются те или иные частицы, зависит от вида этих частиц. В классической статистической физике, созданной Максвеллом и Больцманом, частицы считаются различимыми друг от друга. Такой статистике подчиняются, например, молекулы газа. Известно, что

различных частиц можно распределить по ячейкам способами. Если все эти способов при заданной энергии имеют равную вероятность, то говорят о статистике Максвелла-Больцмана.

Оказалось, что этой статистике подчиняются не все физические объекты. Фотоны, атомные ядра и атомы, содержащие четное число элементарных частиц, подчиняются иной статистике, разработанной Эйнштейном и индийским ученым Бозе. В статистике Бозе-Эйнштейна частицы считаются неразличимыми друг от друга. Поэтому имеет значение лишь то, сколько частиц попало в ту или иную ячейку, а не то, какие именно частицы туда попали.

Однако для многих частиц, например таких как электроны, протоны и нейтроны, не годится и статистика Бозе-Эйнштейна. Для них в каждой ячейке может находится не более одной частицы, причем различные распределения, удовлетворяющие указанному условию, имеют равную вероятность. В этом случае может быть

различных распределений. Эта статистика называется статистикой Дирака-Ферми.

В задачах, которые мы сейчас

В задачах, которые мы сейчас рассмотрим, элементы делятся на группы, и надо найти все способы такого раздела. При этом могут встретиться различные случаи. Иногда существенную роль играет порядок элементов в группах: например, когда сигнальщик вывешивает сигнальные флаги на нескольких мачтах, то для него важно не только то, на какой мачте окажется тот или иной флаг, но и то, в каком порядке эти флаги развешиваются. В других же случаях порядок элементов в группах никакой роли не играет. Когда игрок в домино выбирает кости из кучи, ему безразлично, в каком порядке они придут, а важен лишь окончательный результат.
Отличаются задачи и по тому, играет ли роль порядок самих групп. При игре в домино игроки сидят в определенном порядке, и важно не только то, как разделились кости, но и то, кому какие кости достались. Если раскладывать фотографии по одинаковым конвертам, чтобы разослать их, то существенно, как распределяются фотографии по конвертам, но порядок самих конвертов совершенно несущественен.
Играет роль и то, различаем ли мы между собой сами элементы или нет, а также различаем ли между собой группы, на которые делятся элементы. Наконец, в одних задачах некоторые группы могут оказаться пустыми, то есть не содержащими ни одного элемента, а в других такие группы недопустимы. В соответствии со всем сказанным возникает целый ряд различных комбинаторных задач на разбиение.

Сколькими способами можно сделать такое

Общая постановка этих задач:
Задач 1. Раскладка по ящикам
Даны различных предметов и ящиков. Надо положить в первый ящик предметов, во второй - предметов,..., в -й - предметов, где . Сколькими способами можно сделать такое распределение?
Число различных раскладок по ящикам равно Эту формулу можно получить при решении следующей, на первый взгляд, совсем непохожей задачи:
Задача 2. Перестановки с повторением.
Имеются предметы различных типов. Сколько различных перестановок можно сделать из предметов первого типа, предметов второго типа, ..., предметов -го типа? Число элементов в каждой перестановке равно . Поэтому если бы все элементы были различны, то число перестановок равнялось бы . Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В самом деле, возьмем, например, перестановку

(5.1)

в которой сначала выписаны все элементы первого типа, потом все элементы второго типа, ..., наконец, все элементы -го типа. Элементы первого типа можно переставлять друг с другом способами. Но так как все эти элементы одинаковы, то такие перестановки ничего не меняют. Точно так же ничего не меняют перестановок элементов второго типа, ..., перестановок элементов -го типа.
Перестановки элементов первого типа, второго типа и так далее можно делать независимо друг от друга. Поэтому элементы перестановки 5.1. можно переставлять друг с другом способами так, что она остается неизменной. То же самое верно и для любого другого расположения элементов. Поэтому множество всех перестановок распадается на части, состоящие из одинаковых перестановок каждая. Значит, число различных перестановок с повторениями, которые можно сделать из данных элементов, равно

(5.2)

где .
Пользуясь формулой 5.2, можно ответить на вопрос: сколько перестановок можно сделать из букв слова "Миссисипи"? Здесь у нас одна буква "м", четыре буквы "и", три буквы "с" и одна буква "п", а всего 9 букв. Значит, по формуле 5.2 число перестановок равно Чтобы установить связь между этими задачами, занумеруем все мест, которые могут занимать наши предметы.
Каждой перестановке соответствует распределение номеров мест на классов. В первый класс попадают номера тех мест, на которые попали предметы первого типа, во второй - номера мест предметов второго типа и так далее. Тем самым устанавливается соответствие между перестановками с повторениями и раскладкой номеров мест по "ящикам". Понятно, что формулы решения задач оказались одинаковыми.
В рассмотренных задачах мы не учитывали порядок, в котором расположены элементы каждой части. В некоторых задачах этот порядок надо учитывать.
Задача 3. Флаги на мачтах.
Имеется различных сигнальных флагов и мачт, на которые их вывешивают. Значение сигнала зависит от того, в каком порядке развешены флаги. Сколькими способами можно развесить флаги, если все флаги должны быть использованы, но некоторые из мачт могут оказаться пустыми?
Каждый способ развешивания флагов можно осуществить в два этапа. На первом этапе мы переставляем всеми возможными способами данные флагов. Это можно сделать способами. Затем берем один из способов распределения одинаковых флагов по мачтам (число этих способов ). Пусть этот способ заключается в том, что на первую мачту надо повесить флагов, на вторую - флагов, ..., на -ю флагов, где . Тогда берем первые флагов данной последовательности и развешиваем в полученном порядке на первой мачте; следующие флагов развешиваем на второй мачте и т.д. Ясно, что используя все перестановки флагов и все способы распределения одинаковых флагов по мачтам, получим все способы решения поставленной задачи. По правилу произведения получаем, что число способов развешивания флагов равно

(5.3)

Вообще, если имеется различных вещей, то число способов распределения этих вещей по различным ящикам равно .

Задачи на разбиение чисел

Теперь мы переходим к задачам, в которых все разделяемые предметы совершенно одинаковы. В этом случае можно говорить не о разделении предметов, а о разбиении натуральных чисел на слагаемые (которые, конечно, тоже должны быть натуральными числами).

Здесь возникает много различных задач. В одних задачах учитывается порядок слагаемых, в других - нет.

Задача 4. Отправка бандероли.

За пересылку бандероли надо уплатить 18 рублей. Сколькими способами можно оплатить ее марками стоимостью 4, 6, и 10 рублей, если два способа, отличающиеся порядком марок, считаются различными (запас марок различного достоинства считаем неограниченным)?

Обозначим через

число способов, которыми можно наклеить марки в 4, 6 и 10 рублей так, чтобы общая стоимость этих марок равнялась . Тогда для справедливо следующее соотношение:

(5.4)

Пусть имеется некоторый способ наклейки марок с общей стоимостью , и пусть последней наклеена марка стоимостью 4 рубля. Тогда все остальные марки стоят ( ) рубля. Наоборот, присоединяя к любой комбинации марок общей стоимостью ( ) рубля одну четырехрублевую марку, получаем комбинацию марок стоимостью рублей. При этом из разных комбинаций стоимостью ( ) рублей получается разные комбинации стоимостью рублей. Итак, число искомых комбинаций, где последней наклеена марка стоимостью 4 рубля, равно .

Точно так же доказывается, что число комбинаций, оканчивающихся на на шестирублевую марку, равно

, а на десятирублевую марку оканчиваются комбинацией. Поскольку любая комбинация оканчивается на марку одного из указанных типов, то по правилу суммы получаем соотношение 5.4.

Соотношение 5.4 позволяет свести задачу о наклеивании марок на сумму

рублей к задачам о наклеивании марок на меньшие суммы. Но при малых значениях задачу легко решить непосредственно. Простой подсчет показывает, что Равенство означает, что сумму в 0 рублей можно уплатить единственным образом: совсем не наклеивая марок. А сумму в 1,2,3,5,7 и 9 рублей вообще никак нельзя получить с помощью марок стоимостью 4, 6 и 10 рублей.
Используя значения для , легко найти : После этого находим и т.д. Наконец, получаем значение . Таким образом, марки можно наклеить восемью способами. Эти способы таковы: ; ; ; ; ; ; ; . Отметим, что значения для можно было получить иначе, не приводя непосредственно проверки. Дело в том, что при имеем , поскольку отрицательную сумму нельзя уплатить, наклеивая неотрицательное количество марок. В то же время, как мы видели, . Поэтому .
Точно так же получаем значение , а для имеем .
Задача 5.Общая задача о наклейке марок.
Разобранная задача является частным случаем следующей общей задачи:
Имеются марки достоинством в . Сколькими способами можно оплатить с их помощью сумму в рублей, если два способа, отличающиеся порядком, считаются различными? Все числа различны, а запас марок неограничен. Здесь на первом месте мы будем указывать число слагаемых, на втором – разбиваемое число и на последнем - ограничения на величину слагаемых.
В этом случае число способов удовлетворяет соотношению

(5.5)

При этом , если и . С помощью соотношения 5.5 можно найти для любого , последовательно вычисляя .
Рассмотрим частный случай этой задачи, когда , . Мы получаем всевозможные разбиения числа на слагаемые , причем разбиения, отличающиеся порядком слагаемых, считаются различными. Обозначим число этих разбиений через . (На первом месте мы будем указывать число слагаемых, на втором - разбиваемое число и на последнем – ограничения на величину слагаемых.) Из соотношения 5.5 следует, что

(5.6)

При этом и ,если . Вычисление можно упростить, если заметить, что и потому

(5.7)

Ясно, что слагаемые не могут быть больше . Поэтому равно числу всех разбиений на на натуральные слагаемые (включая и "разбиение" . Если число слагаемых равно , то получаем разбиений. Поэтому Итак, мы доказали, что натуральное число можно разбить на слагаемые способами. Напомним, что при этом учитывается порядок слагаемых.Например, число 5 можно разбить на слагаемые способами.

5 = 5	5 = 3 + 1 + 1	5 = 1 + 2 + 2
5 = 4 + 1	5 = 1 + 3+ 1	5 = 2 + 1 + 1 + 1
5 = 1 + 4	5 = 1 + 1 + 3	5 = 1 + 2 + 1 + 1
5 = 2 + 3	5 = 2 + 2 + 1	5 = 1 + 1 + 2 + 1
5 = 3 + 2	5 = 2 + 1 + 2	5 = 1 + 1 + 1 + 2
		5 = 1 + 1 + 1 + 1 + 1

Формула включений и исключений

Пусть имеется

предметов, некоторые из которых обладают свойствами . При этом каждый предмет может либо не обладать ни одним из этих свойств, либо обладать одним или несколькими свойствами. Обозначим через количество предметов, обладающих свойствами (и быть может, еще некоторыми из других свойств). Если нужно взять предметы, не обладающие некоторым свойством, то эти свойства пишем со штрихом. Например, через ) обозначено количество предметов, обладающих свойствами , но не обладающих свойством (вопрос об остальных свойствах останется открытым). Число предметов, не обладающих ни одним из указанных свойств, обозначается по этому правилу через . Общий закон состоит в том, что

(6.3)

Здесь алгебраическая сумма распространена на все комбинации свойств

(без учета их порядка), причем знак + ставится, если число учитываемых свойств четно, и знак , если это число нечетно. Например, входит со знаком +, а со знаком . Формулу 6.3 называют формулой включений и исключений - сначала исключаются все предметы, обладающие хотя бы одним из свойств , потом включаются предметы, обладающие, по крайней мере, двумя из этих свойств, затем исключаются имеющие, по крайней мере, три и т.д.

Множества и мультимножества

Не существует формального определения множества; считается что это понятие первичное и не определяется. Так, можно говорить, что множество есть объединение различных элементов, но при этом мы оставляем неопределяемыми понятия "объединение" и "элементы". Дадим следующее определение множеству: множество - это неупорядоченная совокупность различных объектов или структура данных, используемая для представления множества. Мультимножество есть объединение не обязательно различных элементов; его можно считать множеством, в котором каждому элементу поставлено в соответствие положительное целое число, называемое кратностью.

Конечное множество

будем записывать в следующем виде:

где

- элементы , обязательно различные! Мощность множества обозначается как , для выписанного выше множества мощность записывается так . Если - конечное мультимножество, то будем записывать его в следующем виде:

Здесь все

различны и - кратность элемента . В этом случае мощность равна

Наиболее общими операциями на множествах и мультимножествах являются операции объединения и пересечения. Для множеств эти операции будем обозначать

и , а для мультимножеств - и . Последовательное и связанное представление последовательностей можно использовать для множеств и мультимножеств очевидным способом. Индуцируя искусственный порядок элементов множества или используя собственный порядок, если он существует, можно рассматривать множество как последовательность. Аналогично, как последовательность можно рассматривать и мультимножество, или, для того чтобы сэкономить место, его можно рассматривать как последовательность пар, каждая из которых состоит из элемента и его кратности.

Как и для последовательностей, наилучший метод представления множеств или мультимножеств существенно зависит от операций, которые выполняются над ними. Предположим, например, что имеем дело с непересекающимися подмножествами множества

и что над ними необходимо выполнить две следующие операции: объединение двух множеств и отыскание подмножества, содержащего данное .
Таким образом, в любой момент времени имеем разбиение на непустые непересекающиеся подмножества. Рассмотрим эти операции в конце данной лекции.

С целью идентификации считаем, что каждое из непересекающихся подмножеств множества имеет имя. Имя - это просто один из элементов подмножества, или, иначе, - представитель подмножества. Когда мы будем ссылаться на имя подмножества, то будем под этим подразумевать его представителя. Рассмотрим, например, множество

разбитое на четыре непересекающихся подмножества

(6.1)

В каждом из подмножеств, взятый в скобки элемент является его именем. Если нам нужно найти подмножество, в котором содержится восьмерка, искомым ответом будет 7, то есть имя подмножества, содержащего восьмерку. Если нужно взять объединение подмножеств с именами 2 и 10, получим разбиение множества

следующего вида:



Именем множества

может быть или 2, или 10.Предполагаем, что вначале имеется разбиение множества

на подмножеств, каждое из которых состоит из одного элемента

(6.2)

и имя каждого из них есть просто этот единственный элемент. Это разбиение преобразуется путем применения операций объединения вперемешку с операциями отыскания. Такая кажущаяся на первый взгляд надуманной задача чрезвычайно полезна в определенных комбинаторных алгоритмах; пример ее полезности виден в "жадном" алгоритме (лекция 16).

Для реализации операций и объединения, и отыскания опишем процедуры (операции) и . Процедура (операция) по именам двух различных подмножеств

и образует новое подмножество, содержащее все элементы множеств и . Процедура (операция)

выдает имя множества, содержащего . Например, если нужно множество,содержащее , объединить с множеством, содержащим , необходимо выполнить следующую последовательность операторов:

Предположим, что мы имеем операций объединения, перемешанных с операциями отыскания, и что начинаем алгоритм с множества , которое разбито на подмножества, состоящие из одного элемента (см. 6.2.). Найдем такую структуру данных для представления непересекающихся подмножеств множества , чтобы последовательность операций можно было производить эффектно.


Такой структурой данных является представление в виде леса с указателями отца, как показано на рис. 4.5 лекции 4. Каждый элемент множества будет узлом леса, а отцом его будет элемент из того же подмножества, что и . Если элемент не имеет отца, то есть является корнем, то он будет именем своего подмножества. В соответствии с этим разбиение 5.1 может быть представлено так:


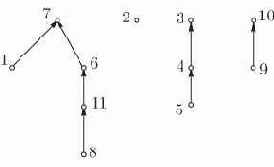
Рис. 6.1.  Представление разбиения

При таком представлении процедура (операция) состоит в переходах по указателям отцов от до корня, то есть имени, его подмножества. Процедура (операция) состоит в связывании вместе некоторым образом деревьев, имеющих корни и . Например, такую связь можно осуществить, сделав отцом .

После операций объединения наибольшее из возможных подмножеств, получающихся в результате разбиения , будет содержать элементов. Поскольку каждое объединение уменьшает число подмножеств на единицу, последовательность операций может содержать не более

объединений, откуда . Так как каждая операция объединения изменяет имя подмножества, содержащего некоторые элементы, можно считать, что каждому объединению предшествует по крайней мере одно отыскание, в связи с чем естественно предположить, что . Выясним, насколько эффективно можно выполнить последовательность из операций объединения, перемешанных с операциями отыскания. Время, требуемое на операции объединения, очевидно, пропорционально , потому что необходимая для каждой операции объединения переделка некоторых указателей требует фиксированного количества работы. Поэтому сосредоточим свое внимание на времени, требуемом для операций отыскания.

Если операция выполняется путем назначения отцом , то после операций объединения может получиться лес, показанный ниже.



В этом случае, если операций отыскания выполняются после всех операций объединения и каждый поиск начинается внизу цепи из элементов множества, то ясно, что время, требуемое на операции отыскания, будет пропорционально . Очевидно, оно не может быть больше, чем константа, умноженная на .Можно существенно уменьшить эту оценку.

Примеры программы

Программа 1. Решето Эратосфена.

{В примере, иллюстрирующем работу с множествами, реализуется алгоритм выделения из первой сотни натуральных чисел всех простых чисел. В основе алгоритма лежит прием "решета Эратосфена". Алгоритм написан на языке программирования Turbo-Pascal.}

Uses crt; Const N=100; {количество элементов исходного множества} Type SetN=set of 1..N; var n1, next, I : word; {вспомогательные переменные } BeginSet, {исходное множество } PrimerSet: SetN; {множество простых чисел } Begin Clrscr; {почистить экран} BeginSet:=[2..N]; {создать исходное множество} PrimerSet:=[1]; {первое простое число} next:=2; {следующее простое число} while BeginSet <> [ ] do {начало основного цикла} begin n1:=next; {n1-число, кратное очередному простому (next)} while n1<=N do {цикл удаления из исходного множества непростых чисел} begin BeginSet:=BeginSet-[n1]; n1:=n1+next {следующее кратное} end; {конец цикла удаления} repeat {получить следующее простое число, которое есть первое не вычеркнутое из исходного множества} inc(next) until(next in BeginSet) or (next > N) end; {конец основного цикла} {вывод результата} textcolor(15); {задание цвета} for I:=1 to N do if i in PrimerSet then write(I:8); readlen; end.

Программа 2. Простые числа в порядке убывания от 200.

{Находит и пишет все простые числа в порядке убывания от 2 до 200. Алгоритм написан на языке программирования Turbo-Pascal.}

Uses crt; const n=197; var

i,q,w,e,r,t:integer; prost:array[1..n] of integer;

begin clrscr; e:=1; r:=0; for q:=1 to n do begin r:=0; for w:=2 to n-1 do if (q<>w) and (q mod w = 0) then r:=1; {prost[e]:=q; e:=e+1;}

if r=0 then begin{begin write(q,' ');}

prost[e]:=q; e:=e+1; end; end;

for i:=e downto 2 do begin write (prost[i],' '); if wherex>70 then writeln;

end; readln; end.

Программа 3. Поиск литер в строке.

{Поиск числа вхождений в данную сроку литер a, c, e, h. Алгоритм написан на языке программирования Turbo-Pascal.}

Uses crt; type liter_set = set of char;

var c:integer; let: liter_set; a:char;

begin clrscr; let:=['a','c','e','h'];

repeat a:=readkey; write(a); if a in let then c:=c+1; until a = '.'; writeln; writeln('Общее число вхожений литер a,c,e,h в вашу запись:',c); readln;

end.

Решето Эратосфена

Одной из самых больших загадок математики является расположение простых чисел в ряду всех натуральных чисел. Иногда два простых числа идут через одно, (например, 17 и 19, 29 и 31), а иногда подряд идет миллион составных чисел. Сейчас ученые знают уже довольно много о том, сколько простых чисел содержится среди

первых натуральных чисел. В этих подсчетах весьма полезным оказался метод, восходящий еще к древнегреческому ученому Эратосфену. Он жил в третьем веке до новой эры в Александрии.

Эратосфен занимался самыми различными вопросами - ему принадлежат интересные исследования в области математики, астрономии и других наук. Впрочем, такая разносторонность привела его к некоторой поверхностности. Современники несколько иронически называли Эратосфена "во всем второй": второй математик после Евклида, второй астроном после Гиппарха и т.д.

В математике Эратосфена интересовал как раз вопрос о том, как найти все простые числа среди натуральных чисел от 1 до

. (Эратосфен считал 1 простым числом. Сейчас математики считают 1 числом особого вида, которое не относится ни к простым, ни к составным числам.) Он придумал для этого следующий способ. Сначала вычеркивают все числа, делящиеся на 2 (исключая само число 2). Потом берут первое из оставшихся чисел (а именно 3). Ясно, что это число - простое. Вычеркивают все идущие после него числа, делящиеся на 3. Первым оставшимся числом будет 5. Вычеркивают все идущие после него числа, делящиеся на 5, и т.д. Числа, которые уцелеют после всех вычеркиваний, и являются простыми. Так как во времена Эратосфена писали на восковых табличках и не вычеркивали, а "выкалывали" цифры, то табличка после описанного процесса напоминала решето. Поэтому метод Эратосфена для нахождения простых чисел получил название "решето Эратосфена".

Подсчитаем, сколько останется чисел в первой сотне, если мы вычеркнем по методу Эратосфена числа, делящиеся на 2, 3 и 5. Иными словами, поставим такой вопрос: сколько чисел в первой сотне не делится ни на одно из чисел 2, 3, 5? Эта задача решается по формуле включения и исключения.

Обозначим через свойство числа делиться на 2, через - свойство делимости на 3 и через - свойство делимости на 5. Тогда

означает, что число делится на 6, означает, что оно делится на 10, и - оно делится на 15. Наконец, означает, что число делится на 30. Надо найти, сколько чисел от 1 до 100 не делится ни на 2, ни на 3, ни на 5, то есть не обладает ни одним из свойств , , . По формуле 6.3 имеем

Но чтобы найти, сколько чисел от 1 до делится на , надо разделить на и взять целую часть получившегося частного. Поэтому





и значит,



Таким образом, 32 числа от 1 до 100 не делятся ни на 2, ни на 3, ни на 5. Эти числа и уцелеют после первых трех шагов процесса Эратосфена. Кроме них останутся сами числа 2, 3 и 5. Всего останется 35 чисел.

А из первой тысячи после первых трех шагов процесса Эратосфена останется 335 чисел. Это следует из того, что в этом случае

Другой метод доказательства

В предыдущем разделе непосредственно установлена связь между задачей Фибоначчи и комбинаторной задачей. Эту связь можно установить и иначе, непосредственно доказав, что число

решений комбинаторной задачи удовлетворяет тому же рекуррентному соотношению

(7.5)

что и числа Фибоначчи. В самом деле, возьмем любую

-последовательность нулей и единиц, удовлетворяющую условию, что никакие две единицы не идут подряд. Она может оканчиваться или на 0, или на 1. Если она оканчивается на 0, то, отбросив его, получим -последовательность, удовлетворяющую нашему условию. Если взять любую - последовательность нулей и единиц, в которой подряд не идут две единицы, и приписать к ней нуль, то получим -последовательность с тем же свойством. Таким образом доказано, что число последовательностей, оканчивающихся на нуль, равно .

Пусть теперь последовательность оканчивается на 1. Так как двух единиц подряд быть не может, то перед этой единицей стоит нуль. Иными словами, последовательность оканчивается на 01. Остающаяся же после отбрасывания 0 и 1

-последовательность может быть любой, лишь бы в ней не шли подряд две единицы. Поэтому число последовательностей, оканчивающихся единицей, равно . Но каждая последовательность оканчивается или на 0, или на 1. В силу правила суммы получаем, что .

Таким образом, получено то же самое рекуррентное соотношение. Отсюда еще не вытекает, что числа

и совпадают.

Перестановки

При составлении размещений без повторений из

элементов по мы получили расстановки, отличающиеся друг от друга и составом, и порядком элементов. Но если брать расстановки, в которые входят все

элементов, то они могут отличаться друг от друга лишь порядком входящих в них элементов. Такие расстановки называют перестановками из n элементов, или, короче,

-перестановками.

Процесс последовательных разбиений

Для решения комбинаторных задач часто применяют метод, использованный в предыдущем пункте: устанавливают для данной задачи рекуррентное соотношение и показывают, что оно совпадает с рекуррентным соотношением для другой задачи, решение которой нам уже известно. Если при этом совпадают и начальные члены последовательностей в достаточном числе, то обе задачи имеют одинаковые решения.

Применим описанный прием для решения следующей задачи.

Пусть дано некоторое множество из

предметов, стоящих в определенном порядке. Разобьем это множество на две непустые части так, чтобы одна из этих частей лежала левее второй (то есть, скажем, одна часть состоит из элементов от первого до

- го, а вторая - из элементов от

-го до

-го). После этого каждую из частей таким же образом разобьем на две непустые части (если одна из частей состоит уже из одного предмета, она не подвергается дальнейшим разбиениям). Этот процесс продолжается до тех пор, пока не получим части, состоящие из одного предмета каждая. Сколько существует таких процессов разбиения (два процесса считаются различными, если хотя бы на одном шагу они приводят к разным результатам)?

Обозначим число способов разбиения для множества из

предметов через

. На первом шагу это множество может быть разбито способами (первая часть может содержать один предмет, два предмета,…, предметов). В соответствии с этим множество всех процессов разбиений распадается на классов - в - класс входят процессы, при которых первая часть состоит из предметов.

Подсчитаем число процессов в

-м классе. В первой части содержится элементов. Поэтому ее можно разбивать далее различными процессами. Вторая же часть содержит элементов, и ее можно разбивать далее

процессами. По правилу произведения получаем, что

- класс состоит из различных процессов. По правилу суммы отсюда вытекает, что

(7.6)

Таким образом получено рекуррентное соотношение для

. Двоичный поиск, поиск делением пополам. Поиском по числам Фибоначчи называется поиск, основанный на том, что область поиска делится в точках, являющихся числами Фибоначчи.

Размещения без повторений

Имеется

различных предметов. Сколько из них можно составить -расстановок? При этом две расстановки считаются различными, если они либо отличаются друг от друга хотя бы одним элементом, либо состоят из одних и тех же элементов, но расположенных в разном порядке. Такие расстановки называют размещениями без повторений, а их число обозначают . При составлении -размещений без повторений из предметов нам надо сделать выборов. На первом шагу можно выбрать любой из имеющихся предметов. Если этот выбор уже сделан, то на втором шагу приходится выбирать из оставшихся предметов. На - м шагу предметов. Поэтому по правилу произведения получаем, что число -размещений без повторения из предметов выражается следующим образом:

Рекуррентные соотношения

При решении многих комбинаторных задач пользуются методом сведения данной задачи к задаче, касающейся меньшего числа предметов. Метод сведения к аналогичной задаче для меньшего числа предметов называется методом рекуррентных соотношений (от латинского "recurrere" - "возвращаться").

Понятие рекуррентных соотношений проиллюстрируем классической проблемой, которая была поставлена около 1202 года Леонардо из Пизы, известным как Фибоначчи. Важность чисел Фибоначчи для анализа комбинаторных алгоритмов делает этот пример весьма подходящим.

Фибоначчи поставил задачу в форме рассказа о скорости роста популяции кроликов при следующих предположениях. Все начинается с одной пары кроликов. Каждая пара становится фертильной через месяц, после чего каждая пара рождает новую пару кроликов каждый месяц. Кролики никогда не умирают, и их воспроизводство никогда не прекращается.

Пусть

- число пар кроликов в популяции по прошествии месяцев, и пусть эта популяция состоит из пар приплода и "старых" пар, то есть . Таким образом, в очередном месяце произойдут следующие события: . Старая популяция в -й момент увеличится на число родившихся в момент времени . . Каждая старая пара в момент времени производит пару приплода в момент времени . В последующий месяц эта картина повторяется:

Объединяя эти равенства, получим следующее рекуррентное соотношение:

(7.1)

Выбор начальных условий для последовательности чисел Фибоначчи не важен; существенное свойство этой последовательности определяется рекуррентным соотношением. Будем предполагать

(иногда ).

Рассмотрим эту задачу немного иначе.

Пара кроликов приносит раз в месяц приплод из двух крольчат (самки и самца), причем новорожденные крольчата через два месяца после рождения уже приносят приплод. Сколько кроликов появится через год, если в начале года была одна пара кроликов?

Из условия задачи следует, что через месяц будет две пары кроликов. Через два месяца приплод даст только первая пара кроликов, и получится 3 пары.
А еще через месяц приплод дадут и исходная пара кроликов, и пара кроликов, появившаяся два месяца тому назад. Поэтому всего будет 5 пар кроликов. Обозначим через

количество пар кроликов по истечении месяцев с начала года. Ясно, что через

месяцев будут эти пар и еще столько новорожденных пар кроликов, сколько было в конце месяца , то есть еще пар кроликов. Иными словами, имеет место рекуррентное соотношение

(7.2)

Так как, по условию, и , то последовательно находим и т.д.

В частности, .

Числа называются числами Фибоначчи. Они обладают целым рядом замечательных свойств. Теперь выведем выражение этих чисел через . Для этого установим связь между числами Фибоначчи и следующей комбинаторной задачей.

Найти число

последовательностей,состоящих из нулей и единиц, в которых никакие две единицы не идут подряд.

Чтобы установить эту связь, возьмем любую такую последовательность и сопоставим ей пару кроликов по следующему правилу: единицам соответствуют месяцы появления на свет одной из пар "предков" данной пары (включая и исходную), а нулями - все остальные месяцы. Например, последовательность 010010100010 устанавливает такую "генеалогию": сама пара появилась в конце 11-го месяца, ее родители - в конце 7-го месяца, "дед" - в конце 5-го месяца и "прадед" - в конце второго месяца. Исходная пара кроликов тогда зашифровывается последовательностью 000000000000.

Ясно, что при этом ни в одной последовательности не могут стоять две единицы подряд - только что появившаяся пара не может, по условию, принести приплод через месяц. Кроме того, при указанном правиле различным последовательностям отвечают различные пары кроликов, и обратно, две различные пары кроликов всегда имеют разную "генеалогию", так как, по условию, крольчиха дает приплод, состоящий только из одной пары кроликов.

Установленная связь показывает, что число -последовательностей, обладающих указанным свойством, равно .

Докажем теперь, что

(7.3)

где , если нечетно, и , если четно.


Иными словами, - целая часть числа ( в дальнейшем будем обозначать целую часть числа через ; таким образом, ).

В самом деле, - это число всех - последовательностей из 0 и 1, в которых никакие две единицы не стоят рядом. Число же таких последовательностей, в которые входит ровно единиц и нулей, равно . Так как при этом должно выполняться неравенство , то изменяется от 0 до . Применяя правило суммы, приходим к соотношению (7.3).

Равенство (7.3) можно доказать и иначе. Положим

где . Из равенства

легко следует, что

(7.4)

Кроме того, ясно, что и. Так как обе последовательности и

удовлетворяют рекуррентному соотношению , то имеем

и, вообще, .

Сочетания

В тех случаях, когда нас не интересует порядок элементов в комбинации, а интересует лишь ее состав, говорят о сочетаниях. Итак,

-сочетаниями из

элементов называют всевозможные

- расстановки, составленные из этих элементов и отличающиеся друг от друга составом, но не порядком элементов. Число -сочетаний, которое можно составить из элементов, обозначают через .

Формула для числа сочетаний получается из формулы для числа размещений. В самом деле, составим сначала все

-сочетания из

элементов, а потом переставим входящие в каждое сочетание элементы всеми возможными способами. При этом получается, что все

-размещения из элементов, причем каждое только по одному разу. Но из каждого - сочетания можно сделать перестановок, а число этих сочетаний равно . Значит справедлива формула Из этой формулы находим, что

Затруднение мажордома"

Бывают комбинаторные задачи, в которых приходится составлять не одно рекуррентное соотношение, а систему соотношений, связывающую несколько последовательностей. Эти соотношения выражают

-у члены последовательностей через предыдущие члены не только данной, но и остальных последовательностей.

Задача: "Затруднение мажордома". Однажды мажордом короля Артура обнаружил, что к обеду за круглым столом приглашено 6 пар враждующих рыцарей. Сколькими способами можно рассадить их так, чтобы никакие два врага не сидели рядом?

Если мы найдем какой-то способ рассадки рыцарей, то, пересаживая их по кругу, получим еще 11 способов. Мы не будем сейчас считать различными способы, получающиеся друг из друга такой циклической пересадкой.

Введем следующие обозначения. Пусть число рыцарей равно

. Через обозначим число способов рассадки, при которых никакие два врага не сидят рядом. Через обозначим число способов, при которых рядом сидит ровно одна пара врагов, и через - число способов, при которых есть ровно две пары враждующих соседей.

Выведем сначала формулу, выражающую

через . Пусть пар рыцарей посажены так, что никакие два врага не сидят рядом. Мы будем считать, что все враждующие пары рыцарей занумерованы. Попросим встать из-за стола пару рыцарей с номером . Тогда возможны три случая: среди оставшихся за столом нет одной пары соседей- врагов, есть одна такая пара и есть две такие пары (ушедшие рыцари могли разделять эти пары). Мы считаем, что . При

последующие рассуждения теряют силу.

Выясним теперь, сколькими способами можно снова посадить ушедших рыцарей за стол так, чтобы после этого не было одной пары соседей-врагов.

Проще всего посадить их, если за столом рядом сидят две пары врагов. В этом случае один из вновь пришедших садится между рыцарями первой пары, а другой – между рыцарями второй пары. Это можно сделать двумя способами. Но так как число способов рассадки

рыцарей, при которых две пары соседей оказались врагами, равно , то всего получилось способов.

Пусть теперь рядом сидит только одна пара врагов.
Один из вернувшихся должен сесть между ними. Тогда за столом окажутся

рыцарей, между которыми есть мест. Из них два места - рядом с только что севшим гостем – запретны для второго рыцаря, и ему остается мест. Так как первым может войти любой из двух вышедших рыцарей, то получается способов рассадки. Но число случаев, когда рыцарей сели так, чтобы ровно одна пара врагов оказалась соседями, ровно . Поэтому мы получаем способов посадить гостей требуемым образом.
Наконец, пусть никакие два врага не сидели рядом. В этом случае первый рыцарь садится между любыми двумя гостями - это он может сделать способами. После этого для его врага останется мест - он может занять любое место, кроме двух мест, соседних с только что севшим рыцарем. Таким образом, если рыцарей уже сидели нужным образом, то вернувшихся гостей можно посадить
способами. Как уже отмечалось, разработанными случаями исчерпываются все возможности. Поэтому имеет место рекуррентное соотношение

(7.7)

Этого соотношения пока недостаточно, чтобы найти для всех значений . Надо еще узнать, как выражаются через .
Предположим, что среди рыцарей оказалась ровно одна пара врагов-соседей. Мы знаем, что это может произойти в случаях. Во избежание ссоры попросим их удалиться из-за стола. Тогда останется рыцарей, причем возможно одно из двух: либо среди оставшихся нет врагов-соседей, либо есть ровно одна пара таких врагов - до ухода покинувших зал они сидели по обе стороны от них и теперь оказались рядом. Во втором случае ушедших можно посадить обратно только на старое место - иначе появится вторая пара враждующих соседей. Но так как рыцарей можно посадить способами так, чтобы была только одна пара враждующих соседей, то мы получаем вариантов (возвратившихся рыцарей можно поменять местами). В первом же случае можно посадить ушедших между любыми двумя рыцарями, то есть
способами, а так как их еще можно поменять местами, то получится способов. Комбинируя их со всеми способами посадки пар рыцарей, при которых нет соседей врагов, получаем способов.


Наконец, номер ушедшей и вернувшейся пары рыцарей мог быть любым от 1 до . Отсюда вытекает, что рекуррентное соотношение для имеет вид

(7.8)

Наконец, разберем случай, когда среди рыцарей было две пары врагов-соседей. Номера этих пар можно выбрать способами. Заменим каждую пару одним новым рыцарем, причем будем считать новых двух рыцарей врагами. Тогда за столом будут сидеть
рыцарей, причем среди них либо не будет ни одной пары врагов-соседей (если новые рыцари не сидят рядом), либо только одна такая пара.
Первый вариант может быть в случаях. Вернуться к исходной компании мы можем 4 способами благодаря возможности изменить порядок рыцарей в каждой паре. Поэтому первый вариант приводит к
способами.
Второй же вариант может быть в случаях. Имеется случаев, когда какая-нибудь пара врагов сидит рядом. Если указать, какая именно пара должна сидеть рядом, получим в раз меньше случаев.
Здесь тоже можно вернуться к исходной компании 4 способами, и мы получаем всего способов. Отсюда вытекает, что при

(7.9)

Мы получили систему рекуррентных соотношений

(7.10)

(7.11)

(7.12)

Они справедливы при . Но простой подсчет показывает, что . Поэтому из соотношений 7.10-7.12 вытекает, что . Продолжая далее, находим, что гостей можно посадить за стол требуемым образом способами.

Линейные рекуррентные соотношения с постоянными коэффициентами

Для решения рекуррентных соотношений общих правил, вообще говоря, нет. Однако существует весьма часто встречающийся класс соотношений, решаемый единообразным методом. Это - рекуррентные соотношения вида

(8.3)

где

- некоторые числа. Такие соотношения называют линейными рекуррентными соотношениями с постоянными коэффициентами.

Сначала рассмотрим, как решаются такие соотношения при

, то есть изучим соотношение вида

(8.4)

Решение этих соотношений основано на следующих двух утверждениях.

Если

и являются решениями рекуррентного соотношения (8.4), то при любых числах и

последовательность

также является решением этого соотношения.

В самом деле, по условию, имеем

Умножим эти равенства на

и соответственно и сложим полученные тождества. Получим, что

А это означает, что

является решением соотношения(8.4).

Если

является корнем квадратного уравнения

то последовательность

является решением рекуррентного соотношения

В самом деле, если

, то и . Подставляя эти значения в соотношение (8.4), получаем равенство

Оно справедливо, так как по условию имеем

. Заметим, что наряду с последовательностью любая последовательность вида

также является решением соотношения (8.4). Для доказательства достаточно использовать утверждение (8.4), положив в нем

Из утверждений 1 и 2 вытекает следующее правило решения линейных рекуррентных соотношений второго порядка с постоянными коэффициентами.

Пусть дано рекуррентное соотношение

(8.5)

Составим квадратное уравнение

(8.6)

которое называется характеристическим для данного соотношения. Если это уравнение имеет два различных корня

, то общее решение соотношения (8.5) имеет вид

Чтобы доказать это правило, заметим сначала, что по утверждению 2

являются решениями нашего соотношения. А тогда по утверждению 1 и является его решением. Надо только показать, что любое решение соотношения (8.5) можно записать в этом виде. Но любое решение соотношения второго порядка определяется значениями . Поэтому достаточно показать, что система уравнений

имеет решение при любых

.
Этими решениями являются



(Случай, когда оба корня уравнения (8.6) совпадут друг с другом, разберем в следующем пункте.)

Пример на доказанное правило.

При изучении чисел Фибоначчи мы пришли к рекуррентному соотношению

(8.7)

Для него характеристическое уравнение имеет вид

Корнями этого квадратного уравнения являются числа

Поэтому общее решение соотношения Фибоначчи имеет вид

(8.8)

(Мы воспользовались сделанным выше замечанием и взяли показатели

вместо ). Мы называли числами Фибоначчи решения соотношения (8.7), удовлетворяющее начальным условиям ( то есть последовательность ). Часто бывает более удобно добавить к этой последовательности вначале числа 0 и 1, то есть рассматривать последовательность Ясно, что эта последовательность удовлетворяет тому же самому рекуррентному соотношению (8.6) и начальным условиям . Полагая в формуле (8.6) , получаем для

систему уравнений



Отсюда находим, что и потому

(8.9)

На первый взгляд кажется удивительным, что это выражение при всех натуральных значениях принимает целые значения.

Производящие функции

В комбинаторных задачах на подсчет числа объектов при наличии некоторых ограничений искомым решением часто является последовательность

, где - число искомых объектов "размерности" . Например, если мы ищем число разбиений числа, то можем принять , если ищем число подмножеств -элементного множества, то и т.д. В этом случае удобно последовательности , поставить в соответствие формальный ряд

(8.12)

называемый производящей функцией для данной последовательности. Название формальный ряд для данной последовательности означает, что (8.12) мы трактуем только как удобную запись нашей последовательности - в данном случае несущественно, для каких (действительных или комплексных) значений переменной

он сходится. Поэтому мы никогда не будем вычислять значение такого ряда для конкретного значения переменной , мы будем только выполнять некоторые операции на таких рядах, а затем определять коэффициенты при отдельных степенях переменной . Для произвольных рядов

мы определим операцию сложения:

(8.13)

операцию умножения на число (действительное или комплексное):

(8.14)

и произведение Коши

(8.15)

где

(8.16)

Если

для , то ряд (8.12) будем отождествлять с многочленом . Из математического анализа известно, что если ряд (8.12) сходится в некоторой окрестности нуля, то его сумма является аналитической функцией в этой окрестности и

(8.17)

(

обозначает значение -й производной функции для ; ряд 8.12 - это не что иное, как ряд Маклорена функции ). Более того, когда являются аналитическими функциями в окрестности нуля, то формулы (8.13)-(8.16) будут справедливы, если трактовать как значения функций в точке , а ряды понимать в обычном смысле, т.е. так, как в математическом анализе. Это сохраняющее операции взаимно однозначное соответствие между рядами, сходящимися в окрестности нуля, и функциями, аналитическими в окрестности нуля, позволяет отождествить формальный ряд (8.12) с определенной через него аналитической функцией в случае рядов, сходящихся в окрестности нуля (несмотря на то, что ряды мы будем трактовать всегда как формальные ряды, то есть только как формальную запись их коэффициентов). Таким образом, будем писать, например,

и т.д.

Решение рекуррентных соотношений

Будем говорить, что рекуррентное соотношение имеет порядок

, если оно позволяет выразить через . Например,

рекуррентное соотношение второго порядка, а

- рекуррентное соотношение третьего порядка. Если задано рекуррентное соотношение -го порядка, то ему удовлетворяет бесконечно много последовательностей. Дело в том, что первые

элементов последовательности можно задать совершенно произвольно - между ними нет никаких соотношений. Но если первые

элементов заданы, то все остальные элементы определяются совершенно однозначно - элемент выражается в силу рекуррентного соотношения через элемент - через и т.д.

Пользуясь рекуррентным соотношением и начальными членами, можно один за другим выписывать члены последовательности, причем рано или поздно получим любой ее член. Однако при этом придется выписать и все предыдущие члены - ведь не узнав их, мы не узнаем и последующих членов. Но во многих случаях нужно узнать только один определенный член последовательности, а остальные не нужны. В этих случаях удобнее иметь явную формулу для

-го члена последовательности. Некоторая последовательность является решением данного рекуррентного соотношения, если при подстановке этой последовательности соотношение тождественно выполняется. Например, последовательность

является одним из решений рекуррентного соотношения

В самом деле, общий член этой последовательности имеет вид

. Значит, . Но при любом имеет место тождество . Поэтому является решением указанного соотношения.

Решение рекуррентного соотношения

-го порядка называется общим, если оно зависит от произвольных постоянных

и путем подбора этих постоянных можно получить любое решение данного соотношения. Например, для соотношения

(8.1)

общим решением будет

(8.2)

В самом деле, легко проверить, что последовательность (8.2) обращает (8.1) в тождество. Поэтому нам надо только показать, что любое решение нашего соотношения можно представить в виде (8.2). Но любое решение соотношения (8.1) однозначно определяется значениями

и . Поэтому нам надо доказать, что для любых чисел и

найдутся такие значения и , что и
Но легко видеть, что при любых значениях и
система уравнений
имеет решение. Поэтому (8.2) действительно является общим решением соотношения (8.1).

Случай равных корней характеристического уравнения

Рассмотрим случай, когда оба корня характеристического уравнения совпадают:

. В этом случае выражение уже не будет общим решением. Ведь из-за того, что , это решение можно записать в виде

Остается только одно произвольное постоянное ; и выбрать его так, чтобы удовлетворить двум начальным условиям

, вообще говоря, невозможно.Поэтому надо найти какое-нибудь второе решение, отличное от . Таким решением является . В самом деле, если квадратное уравнение имеет два совпадающих корня , то по теореме Виета . Поэтому уравнение записывается так:

А тогда рекуррентное соотношение имеет такой вид:

(8.10)

Проверим, что

действительно являются его решением. Имеем , а . Подставляя эти значения в соотношение (8.10), получаем очевидное тождество

Значит,

- решение рассматриваемого соотношения.

Итак, имеются два решения

и заданного соотношения. Его общее решение запишется так:Теперь уже путем подбора можно удовлетворить любым начальным условиям.

Линейные рекуррентные соотношения с постоянными коэффициентами, порядок которых больше двух, решаются таким же способом. Пусть соотношение имеет вид

(8.11)

Составим характеристическое уравнение

Если все корни

этого алгебраического уравнения -й степени различны, то общее решение соотношения (8.3) имеет вид

Если же, например,

, то этому корню соответствуют решения

рекуррентного соотношения (8.11). В общем решении этому корню соответствует часть

Составляя такое выражение для всех корней и складывая их, получаем общее решение соотношения (8.3).

Например, решим рекуррентное соотношение

Характеристическое уравнение в этом случае имеет вид

Решая его, получим корни

Значит, общее решение нашего соотношения имеет следующий вид:

Алгебраические дроби и степенные ряды

При делении многочлена

на многочлен мы получаем бесконечный степенной ряд. Возникает вопрос: как связан этот ряд с алгебраической дробью , то есть какой смысл можно придать записи

(9.2)

Рассмотрим, например, разложение

(9.3)

Мы не пишем здесь знака равенства, так как не знаем, какой смысл имеет стоящая справа сумма бесконечного числа слагаемых. Чтобы выяснить это, попробуем подставлять в обе части соотношения (9.3) различные значения

. Сначала положим . Тогда левая часть соотношения примет значение , а правая превратится в бесконечный числовой ряд

Так как мы не умеем складывать бесконечно много слагаемых, попробуем взять сначала одно слагаемое, потом - два, потом - три и так далее слагаемых. Мы получим такие суммы:

. Ясно, что с возрастанием

эти суммы приближаются к значению

которое приняла левая часть соотношения (9.3) при .

То же самое получится, если вместо

подставить в обе части (9.3) число . Левая часть равенства примет значение 2, а правая превратится в бесконечный числовой ряд Беря последовательно одно, два, три, четыре, слагаемых, мы получим числа 1; ; ; ,…, . Ясно, что с возрастанием эти числа стремятся к числу 2.

Однако, если взять

, то левая часть (9.3) примет значение , а в правой получим ряд

Если последовательно складывать члены этого ряда, то получаются суммы 1; 5; 21; 85; … Эти суммы неограниченно увеличиваются и не приближаются к числу

.

Мы встретились, таким образом, с двумя случаями. Чтобы их различать, введем общее понятие о сходимости и расходимости числового ряда. Пусть задан бесконечный числовой ряд

(9.4)

Говорят, что бесконечный числовой ряд сходится к числу

, если разность

стремится к нулю при неограниченном увеличении

. Иными словами, какое бы число мы ни указали, отклонение суммы от , начиная с некоторого номера , окажется меньше :

В этом случае число

называют суммой бесконечного ряда и пишут

Если не существует числа

, к которому сходится данный ряд (9.4), то этот ряд называют расходящимся.

Проведенное выше исследование показывает, что

в то время как ряд ... расходится. Более тщательное исследование показывает, что если , то ряд сходится к , а если , то он расходится. Чтобы доказать это утверждение, достаточно заметить, что



и что при выражение стремится к нулю, если , и к бесконечности, если . При

получаем расходящиеся числовые ряды

и .Итак, если , то

(9.5)

Отметим, что равенство (9.5) - это известная из школьного курса математики формула для суммы бесконечно убывающей геометрической прогрессии.

Мы выяснили, таким образом, смысл записи

Она показывает, что для значений , лежащих в некоторой области, а именно при , стоящий справа ряд сходится к . Говорят, что функция при разлагается в степенной ряд .Теперь уже можно выяснить и более общий вопрос.

Пусть при делении многочлена на многочлен получился степенной ряд

(9.6)

Оказывается, что тогда при достаточно малых значениях ряд (9.6) сходится к . Размеры области сходимости зависят от корней знаменателя, то есть чисел, при которых знаменатель обращается в нуль. Именно, если эти числа равны и - наименьшее из чисел , то ряд сходится в области .

Иными словами, всегда есть область , в которой выполняется равенство

(9.7)

В степенные ряды можно разлагать не только алгебраические дроби, но и многие другие функции. В математическом анализе доказывают, например, что







Отметим еще следующее важное утверждение: функция

не может иметь двух различных разложений в степенные ряды.

Действия над степенными рядами

Перейдем теперь к действиям над степенными рядами. Пусть функции

и разложены в степенные ряды

(9.12)

(9.13)

Тогда

Оказывается, что слагаемые в правой части равенства можно переставить и сгруппировать вместе члены с одинаковыми степенями

. Это утверждение совсем не так очевидно, как кажется на первый взгляд. Ведь в правой части равенства у нас бесконечные суммы, а в бесконечных суммах переставлять слагаемые можно далеко не всегда. После этой перегруппировки мы получим

(9.14)

Ряд, стоящий в правой части равенства (9.14), называется суммой степенных рядов (9.12) и (9.13).

Посмотрим теперь, как разлагается в степенной ряд произведение функций

и . Мы имеем

(9.15)

Оказывается, что как и в случае многочленов, ряды, стоящие в правой части равенства (9.15), можно почленно перемножать. Мы опускаем доказательство этого утверждения. Найдем ряд, получающийся после почленного перемножения. Свободный член этого ряда равен

. Члены, содержащие , получатся дважды: при умножении на и при умножении на . Они дают

Точно так же вычисляются члены, содержащие

. Таким образом,

(9.16)

Ряд, стоящий в правой части равенства (9.16), называется произведением рядов(9.12) и (9.13).

В частности, возводя ряд (9.12) в квадрат, получаем

(9.17)

Посмотрим теперь, как делят друг на друга степенные ряды. Пусть свободный член ряда (9.13) отличен от нуля. Покажем, что в этом случае существует такой степенной ряд

(9.18)

что

(9.19)

Для доказательства перемножим ряды в левой части этого равенства. Мы получим ряд

Для того чтобы этот ряд совпадал с рядом (9.12), необходимо и достаточно, чтобы выполнялись равенства

Эти равенства дают бесконечную систему уравнений для отыскания коэффициентов Из первого уравнения системы получаем

. Подставим полученное значение во второе уравнение. Мы получим уравнение

из которого находим, что

. Вообще, если уже найдены коэффициенты , то для отыскания имеем уравнение

Это уравнение разрешимо, поскольку

.Итак, мы доказали существование ряда (9.18), удовлетворяющего соотношению (9.19). Ряд (9.18) называют частным при делении рядов (9.12) и (9.13). Можно доказать, что он получается при разложении функции . Таким образом, степенные ряды можно складывать, умножать и делить (последнее - при условии, что свободный член делителя отличается от нуля). Эти действия соответствуют действиям над разлагаемыми функциями.

Деление многочленов

Если заданы два многочлена

и , то всегда существуют многочлены (частное) и (остаток), такие, что , причем степень меньше степени или . При этом называется делимым, а - делителем. Если же мы хотим, чтобы деление выполнялось без остатка, то придется допустить в качестве частного не только многочлены, но и бесконечные степенные ряды. Для получения частного надо расположить многочлены по возрастающим степеням и делить "углом", начиная с младших членов. Рассмотрим, например, деление на

Ясно, что процесс деления никогда не закончится ( так же, например, как при обращении числа

в бесконечную десятичную дробь). С помощью индукции легко убедиться, что все коэффициенты частного равны единице. Поэтому в качестве частного получается бесконечный ряд . Вообще, если и - два многочлена

причем свободный член

многочлена

отличен от нуля,

, то при делении

на

получается бесконечный ряд

(9.1)

Лишь в случае, когда

делится без остатка на , ряд (9.1) обрывается и мы получаем многочлен.

Метод рекуррентных соотношений позволяет решать

Метод рекуррентных соотношений позволяет решать многие комбинаторные задачи. Но в целом ряде случаев рекуррентные соотношения довольно трудно составить, а еще труднее решить. Зачастую эти трудности удается обойти, использовав производящие функции. Поскольку понятие производящей функции связано с бесконечными степенными рядами, познакомимся с этими рядами.

Бином Ньютона

Получим производящую функцию для конечной последовательности чисел

. Известно, что

и

Эти равенства являются частными случаями более общей формулы, дающей разложение для

. Запишем в виде

(10.4)

Раскроем скобки в правой части этого равенства, причем будем записывать все множители в том порядке, в котором они нам встретятся. Например,

запишем в виде

(10.5)

а

- в виде

(10.6)

Видно, что в формулу (10.5) входят все размещения с повторениями, составленные из букв

и по две буквы в каждом размещении, а в формулу (10.6) - размещения с повторениями из тех же букв, но состоящие из трех букв каждое. То же самое и в общем случае — после раскрытия скобок в формуле (10.4) мы получим всевозможные размещения с повторениями букв и , состоящие из элементов. Приведем подобные члены. Подобными будут члены, содержащие одинаковое количество букв (тогда и букв в них будет поровну). Найдем, сколько будет членов, в которые входит

букв

и, следовательно, букв . Эти члены являются перестановками с повторениями, составленными из букв

и

букв . Поэтому их число равно

Отсюда вытекает, что после приведения подобных членов выражение

войдет с коэффициентом . Итак, мы доказали, что

(10.7)

Равенство (10.7) принято называть формулой бинома Ньютона. Если положить в этом равенстве

, то получим

(10.8)

Мы видим, что

является производящей функцией для чисел , . С помощью этой производящей функции можно сравнительно просто доказать многие свойства чисел .

Об едином нелинейном рекуррентном соотношении

При решении задачи о разбиении последовательности мы пришли к рекуррентному соотношению

(10.14)

где

.Покажем, как решить соотношение (10.14). Для этого составим производящую функцию.

(10.15)

Положим

(10.16)

и возведем

в квадрат. Мы получим, что

Но по рекуррентному соотношению (10.14),

Значит,

Полученный ряд есть не что иное, как

; поскольку , он равен

Для функции

получилось квадратное уравнение (10.17). Решая его, находим, что

Мы выбрали перед корнем знак минус, так как в противном случае при

мы имели бы

, а из разложения (10.16) видно, что .

Применение степенных рядов для доказательства тождеств

С помощью степенных рядов можно доказывать многие тождества. Для этого берут некоторую функцию и двумя способами разлагают ее в степенной ряд. Поскольку функция может быть представлена лишь единственным образом в виде степенного ряда, то коэффициенты при одинаковых степенях

в обоих рядах должны совпадать. Это и приводит к доказываемому тождеству.

Рассмотрим, например, известное нам разложение

Возведя обе части этого разложения в квадрат, получаем

(10.1)

Если заменить здесь

на –, то получим, что

(10.2)

Перемножив разложения (10.1) и (10.2), выводим, что

(10.3)

Очевидно, что коэффициенты при нечетных степенях

обращаются в нуль, каждое слагаемое дважды входит в эти коэффициенты с противоположными знаками. Коэффициент же равен

Но функцию

можно разложить в степенной ряд и иным образом. Мы имеем

А разложение для

получается из разложения (10.1), если заменить в нем на :

(10.4)

Мы знаем, что никакая функция не может иметь двух различных разложений в степенные ряды. Поэтому коэффициент при

разложении (10.3) должен равняться коэффициенту при

в разложении (10.4). Отсюда вытекает следующее тождество:

---

---