Производящие функции
Пусть дана некоторая последовательность чисел


Если этот ряд сходится в какой-то области к функции



вытекает, что функция


производящей является функция

Нас будут интересовать производящие функции для последовательностей

Производящие функции и рекуррентные соотношения
Теория производящих функций тесно связана с рекуррентными соотношениями. Вернемся снова к делению многочленов. Пусть функции




- два многочлена, причем



 |
(10.10) |
то


Раскроем в правой части этого равенства скобки и сравним коэффициенты при одинаковых степенях


 |
(10.11) |
(если


 |
(10.12) |
(ведь в




Обратно, если дано рекуррентное соотношение (10.12) и заданы члены



 |
(10.13) |
На первый взгляд кажется, что мы мало выиграли при замене рекуррентного соотношения производящей функции. Ведь все равно придется делить числитель на знаменатель, а это приведет к тому же самому рекуррентному соотношению (10.12). Но дело в том, что над дробью (10.13) можно выполнять некоторые алгебраические преобразования, а это облегчит отыскание чисел

Ряд Ньютона
Мы назвали, как это обычно делают, формулу






 |
(10.9) |
Только теперь получилось не конечное число слагаемых, а бесконечный ряд. В случае, когда


обращается в нуль. Но эта скобка входит в коэффициент всех членов, начиная с


Двоичные деревья
Основные определения и понятия о графах даются в лекции 12.
В лекции 16 и 17 рассматриваются комбинаторные алгоритмы на графах. В данной лекции приведены несколько понятий, необходимых для описания абстрактной структуры данных, - двоичное дерево.
При решении многих задач математики используется понятие графа.Граф - набор точек на плоскости (эти точки называются вершинами графа), некоторые из которых соединены отрезками (эти отрезки называются ребрами графа). Вершины могут располагаться на плоскости произвольным образом. Причем неважно, является ли ребро, соединяющее две вершины, отрезком прямой или кривой линией. Важен лишь факт соединения двух данных вершин графа ребром. Примером графа может служить схема линий железных дорог. Если требуется различать вершины графа, их нумеруют или обозначают разными буквами. В изображении графа на плоскости могут появляться точки пересечения ребер, не являющиеся вершинами.
Говорят, что две вершины графа соединены путем, если из одной вершины можно пройти по ребрам в другую вершину. Путей между двумя данными вершинами может быть несколько. Поэтому обычно путь обозначают перечислением вершин, которые посещают при движении по ребрам. Граф называется связным, если любые две его вершины соединены некоторым путем.
Состоящий из различных ребер замкнутый путь называется циклом. Связный граф, в котором нет циклов, называется деревом. Одним из основных отличительных свойств дерева является то, что в нем любые две вершины соединены единственным путем. Дерево называется ориентированным, если на каждом его ребре указано направление. Следовательно, о каждой вершине можно сказать, какие ребра в нее входят, а какие - выходят. Точно так же о каждом ребре можно сказать, из какой вершины оно выходит, и в какую - входит. Двоичное дерево - это такое ориентированное дерево, в котором:
Имеется ровно одна вершина, в которую не входит ни одного ребра. Эта вершина называется корнем двоичного дерева.В каждую вершину, кроме корня, входит одно ребро.Из каждой вершины (включая корень) исходит не более двух ребер.
Граф задается аналогично спискам через записи и указатели.
Программа 4. Создание и работа с деревом.
//Алгоритм реализован на языке Turbo-C++. //Вершины дерева задаются структурой: поле целых, //поле для размещения адреса левого "сына" и поле для размещения //адреса правого "сына" //Значение целого выбирается случайным образом из интервала 0..99. //Число уровней дерева равно N. В примере N = 5. #include <stdio.h> #include <conio.h> #include <stdlib.h> #include <time.h> #define N 5 struct tree{int a; tree* left; tree* right;};
void postr(tree* root,int h) { root->a=random(100); if (h!=0){ if (random(3)){ root->left=new(tree); postr(root->left,h-1);} else root->left=NULL; if (random(3)) {root->right=new(tree);postr(root->right,h-1);} else root->right=NULL;} else {root->right=NULL;root->left=NULL;} }
void DFS(tree* root) {printf("%d ",root->a); if (root->left!=NULL) DFS(root->left); if (root->right!=NULL) DFS(root->right);}
void main() {clrscr(); randomize(); tree* root1; root1=new(tree); postr(root1,N); DFS(root1); getch(); }

Очереди
Очередь - одномерная структура данных, для которой загрузка или извлечение элементов осуществляется с помощью указателей начала извлечения (head) и конца (tail) очереди в соответствии с правилом FIFO ("first-in, first-out" - "первым введен, первым выведен").
Начальная установка:
Head:=1; tail:=1; Добавление элемента x:
Queue[tail]:=x; tail:=tail+1; If tail>qd then tail:=1; Здесь qd - размерность очереди. Исключение элемента x:
x:=queue[head]; head:=head+1; if head>qd then head:=1; Проверка переполнения очереди и включение в нее элемента:
Temp:=tail+1; If temp>qd then temp:=1; If temp=head then \{переполнение\} Else btgin queue[tail]:=x; tail:=temp end; Проверка элементов и исключение элемента:
If head:=tail then \{очередь пуста\} else begin x:=queue[head]; head:=head+1; if yead>qd then head:=1; end;
Отметим, что при извлечении элемента из очереди все элементы могут также перемещаться на один шаг к ее началу.
Стеки
Стеком называется одномерная структура данных, загрузка или увеличение элементов для которой осуществляется с помощью указателя стека в соответствии с правилом LIFO ("last-in, first-out" "последним введен,первым выведен").
Указатель стека sp (stack pointer) содержит в любой момент времени индекс (адрес) текущего элемента, который является единственным элементом стека, доступным в данный момент времени для обработки.
Существуют следующие основные базисные операции для работы со стеком (для случая, когда указатель стека всегда задает ячейку, находящуюся непосредственно над его верхним элементом).
Начальная установка:
Sp:=1;
Загрузка элемента x в стек:
Stack[sp]:=x; Sp:=sp+1; Извлечение элемента из стека:
Sp:=sp-1; X:=stack[sp]; Проверка на переполнение и загрузка элемента в стек:
If sp<=sd then Begin stack[sp]:=x; sp:=sp+1 end Else \{ переполнение \}; Здесь sd - размерность стека. Проверка наличия элементов и извлечение элемента стека:
If sp>1 then Begin sp:=sp-1; x:=stack[sp] end Else \{ антипереполнение \} Чтение данных из указателя стека без извлечения элемента:
x:=stack[sp-1].
Программа 1. Работа со стеком.
{Реализованы основные базисные операции для работы со стеком. Программа написана на языке программирования Turbo-Pascal }
uses crt,graph; type PEl=^El; El=record n:byte; next:PEl; end;
var ster:array[1..3] of PEl; number: byte; p:PEl; th,l: integer; i:integer; nhod:word; s:string;
procedure hod(n,f,t:integer); begin if n>1 then begin hod(n-1,f,6-(f+t)); hod(1,f,t); hod(n-1,6-(f+t),t); end else begin p:=ster[f]; ster[f]:=ster[f]^.next; p^.next:=ster[t]; ster[t]:=p; inc(nhod); str(nhod,s); {**********************************************************} setfillstyle(1,0);bar(0,0,50,10); setcolor(2);outtextxy(0,0,s); setfillstyle(1,0);setcolor(0);p:=ster[f];i:=1; while p<>nil do begin p:=p^.next;inc(i);end; fillellipse(160*f,460-(i-1)*th,(number-ster[t]^.n+1)*l,10); setfillstyle(1,4);setcolor(4);p:=ster[t];i:=1; while p<>nil do begin fillellipse(160*t,460-(i-1)*th,(number- ster[t]^.n+1)*l,10);inc(i);p:=p^.next;end; {**********************************************************} { readkey;}{delay(50);} end; end;
procedure start; var i:integer;grD,grM: Integer; begin clrscr;write(' Enter the number of rings, please.');readln(number); for i:=1 to 3 do ster[i]:=nil; for i:=1 to number do begin new(p);p^.n:=i;p^.next:=ster[1];ster[1]:=p;end; nhod:=0; grD:=Detect;{InitGraph(grD,grM,'');}InitGraph(grD,grM,'c:\borland\tp\bgi'); th:=20;l:=round(50/number); setfillstyle(1,4);setcolor(4); for i:=1 to number do begin fillellipse(160,460-(i-1)*th,(number- i+1)*l,10);end; end;
begin start; {readkey;} hod(number,1,3); {closegraph;} end.
Программа 2. Ханойская башня.
На стержне


дисков, уменьшающихся по размеру снизу вверх. Диски должны быть переставлены на стержень в исходном порядке при использовании в случае необходимости промежуточного стержня

Программа реализована с помощью абстрактного типа данных – стек для произвольного числа дисков.
{Программа написана на языке программирования Turbo-Pascal}
uses crt,graph; type PEl=^El; El=record n:byte; next:PEl; end;
var ster:array[1..3] of PEl; number: byte; p:PEl; th,l: integer; i:integer; nhod:word; s:string;
procedure hod(n,f,t:integer); begin if n>1 then begin hod(n-1,f,6-(f+t)); hod(1,f,t); hod(n-1,6-(f+t),t); end else begin p:=ster[f]; ster[f]:=ster[f]^.next; p^.next:=ster[t]; ster[t]:=p; inc(nhod); str(nhod,s); {**********************************************************} setfillstyle(1,0);bar(0,0,50,10); setcolor(2);outtextxy(0,0,s); setfillstyle(1,0);setcolor(0);p:=ster[f];i:=1; while p<>nil do begin p:=p^.next;inc(i);end; fillellipse(160*f,460-(i-1)*th,(number-ster[t]^.n+1)*l,10); setfillstyle(1,4);setcolor(4);p:=ster[t];i:=1; while p<>nil do begin fillellipse(160*t,460-(i-1)*th,(number- ster[t]^.n+1)*l,10);inc(i);p:=p^.next;end; {**********************************************************} { readkey;}{delay(50);} end; end;
procedure start; var i:integer;grD,grM: Integer; begin clrscr;write('Enter the number of rings, please.');readln(number); for i:=1 to 3 do ster[i]:=nil; for i:=1 to number do begin new(p);p^.n:=i;p^.next:=ster[1];ster[1]:=p;end; nhod:=0; grD:=Detect;{InitGraph(grD,grM,'');}InitGraph(grD,grM,'c:\borland\tp\bgi'); th:=20;l:=round(50/number); setfillstyle(1,4);setcolor(4); for i:=1 to number do begin fillellipse(160,460-(i-1)*th,(number- i+1)*l,10);end; end;
begin start; {readkey;} hod(number,1,3); {closegraph;} end.
Связанные списки
Связанный список представляет собой структуру данных, которая состоит из узлов (как правило, записей), содержащих указатели на следующий узел. Указатель, который ни на что не указывает, снабжается значением nil. Таким образом, в каждый элемент связанного списка добавляется указатель (звено связи).
Приведем основные базисные операции для работы с однонаправленным связанным списком.
Включение элемента после элемента:
Link[q]:=link[p]; Link[p]:=q;
Здесь q – индекс элемента, который должен быть вставлен в список после элемента с индексом p.
Исключение преемника элемента x:
If link[x]<>null then Link[x]:=[link[x]] else \{Элемент x не имеет преемника\};
Отметим, что элемент, следующий в списке за элементом x, называется преемником элемента x, а элемент, pасположенный перед элементом x, называется предшественником элемента x. Если элемент x не имеет преемника, то содержащемуся в нем указателю присваивается значение nil.
Включение элемента y перед элементом x:
Prev:=0; While(link[prev]<>nil)and(link[prev]<>x)do Prev:=link[prev]; If link[prev]=x then Btgin link[prev]:=y; link[y]:=x end Else \{Элемент x не найден\}; Здесь link[0]является началом списка.
Отметим, что исключение последнего элемента из однонаправленного списка связано с просмотром всего списка.
В двунаправленном связанным списке каждый элемент имеет два указателя (succlink - описывает связь элемента с преемником, predlink - с предшественником).
Приведем основные базисные операции для работы с двунаправленным связанным списком.
Ответ 1Включение y перед элементом x:
Succlink[y]:=x; Predlink[y]:=predlink[x]; Succlink[predlink[x]]:=y; Predlink[x]:=y;
Ответ 2Включение элемента y после элемента x:
Succlink[y]:=succlink[x]; Predlink[y]:=x; Predlink[succlink[x]]:=y; Succlink[x]:=y;
Ответ 3Исключение элемента x.
Predlink[succlink[x]]:=predlink[x]; Succlink[predlink[x]]:=succlink[x];
Программа 3.Список целых чисел.
{Создается список целых чисел. Числа выбираются случайным образом из интервала 0..9999, затем он упорядочивается, сначала - по возрастанию, затем - по убыванию.
Программа написана на языке программирования Turbo-Pascal}
uses crt; type TLink=^Link; Link=record v : integer; p, n : TLink end;
var i : integer; p, q, w : TLink; s1,s2,rs : TLink;
procedure Sort( sp : TLink; t : integer ); var temp : integer; begin q:=sp; while q^.n<>nil do begin q:=q^.n; p:=sp; while p^.n<>nil do begin if (p^.v-p^.n^.v)*t>0 then begin temp:=p^.v; p^.v:=p^.n^.v; p^.n^.v:=temp; end; p:=p^.n; end; end; end;
function CreatRndSpis(deep : integer):TLink; begin new(q); for i:=1 to deep do begin if i=1 then begin p:=q;q^.p:=nil; end; q^.v:=random(9999); new(q^.n); q^.n^.p:=q; q:=q^.n; end; q^.p^.n:=nil; dispose(q); CreatRndSpis:=p; end;
function CreatSortDawnSpis(deep : integer):TLink; begin if deep<9999 then begin new(q); for i:=1 to deep do begin if i=1 then begin q^.p:=nil;p:=q; end; q^.v:=random(round(9999/deep))+round(9999*(1-i/deep)); new(q^.n); q^.n^.p:=q; q:=q^.n; end; q^.p^.n:=nil; dispose(q); end else p:=nil; CreatSortDawnSpis:=p; end;
procedure Show( s : TLink; sp: integer ); var i : integer; begin p:=s; i:=1; while p<>nil do begin gotoxy(sp,i);write(' ' : 5); gotoxy(sp,i);writeln(p^.v); p:=p^.n; inc(i); end; end;
function min( c1, c2 : integer) : integer; begin case c1<c2 of true : min:=c1; false: min:=c2; end; end;
function CreatConcSortUpSpis( sp1, sp2 : TLink ) : TLink; begin q:=sp1;while q^.n<>nil do q:=q^.n; w:=sp2;while w^.n<>nil do w:=w^.n; new(p);
CreatConcSortUpSpis:=p; p^.p:=nil; while(w<>nil)and(q<>nil)do begin if(w<>nil)and(q<>nil)then begin p^.v:=min(q^.v,w^.v); case p^.v=q^.v of true : q:=q^.p; false: w:=w^.p; end; new(p^.n); p^.n^.p:=p; p^.n^.n:=nil; p:=p^.n; end; if(w=nil)and(q<>nil)then begin while q<>nil do begin p^.v:=q^.v;q:=q^.p; new(p^.n); p^.n^.p:=p; p^.n^.n:=nil; p:=p^.n; end; end; if(w<>nil)and(q=nil)then begin while w<>nil do begin p^.v:=w^.v;w:=w^.p; new(p^.n); p^.n^.p:=p; p^.n^.n:=nil; p:=p^.n; end; end; end; p^.p^.n:=nil; dispose(p); end;
begin clrscr; randomize; s1:=CreatRndSpis(15);Sort(s1,-1); s2:=CreatRndSpis( 5);Sort(s2,-1); rs:=CreatConcSortUpSpis(s1,s2); Show(s1,10); Show(s2,20); Show(rs,30); Sort(rs,-1); Show(rs,40); readln; end.
Вирт определил программирование как алгоритм
Н. Вирт определил программирование как алгоритм + структуры данных. При этом структура данных может не зависеть от конкретных языковых конструкций (абстрактная структура данных).
Рассмотрим некоторые основные структуры данных.
Изоморфизм
Два графа












Заметим, что можно ограничится орграфами. Любой неориентированный граф превращается в орграф заменой каждого ребра двумя противоположно направленными ребрами. Два полученные таким образом орграфа, очевидно, изоморфны тогда и только тогда, если изоморфны исходные графы.
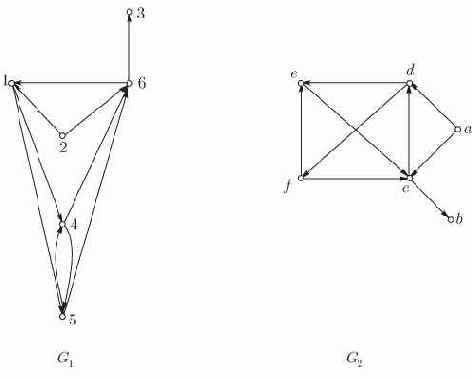
Рис. 12.3. Изоморфные орграфы
Клики
Максимальный полный подграф графа



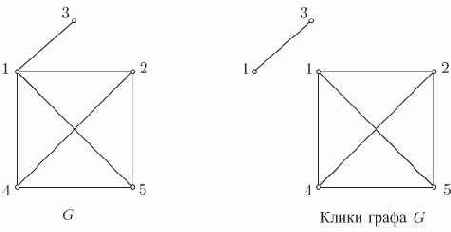
Рис. 12.2. Граф G и все его клики
Клики графа представляют "естественные" группировки вершин, и определение клик графа полезно в кластерном анализе в таких областях, как информационный поиск и социология.
Остовные деревья
Связный неориентированный ациклический граф называется деревом, множество деревьев называется лесом. В связном неориентированном графе











Особый интерес представляют остовные деревья графа





Во взвешенном графе



Жадный алгоритм может быть выполнен в два этапа. Сначала ребра сортируются по весу и затем строится остовное дерево путем выбора наименьших из имеющихся в распоряжении ребер.
Существует другой метод получения минимума остовных деревьев, который не требует ни сортировки ребер, ни проверки на цикличность на каждом шаге, - так называемый алгоритм ближайшего соседа.
Мы начинаем с некоторой произвольной вершины











Наихудшим для этого алгоритма будет случай, когда











Планарность
Граф называют планарным, если существует такое изображение на плоскости его вершин и ребер, что:
каждая вершина




Определение планарности графа отличается от других рассмотренных нами задач, поскольку при изображении точек и линий на плоскости приходится больше иметь дело с непрерывными, а не с дискретными величинами. Взаимосвязь между дискретными и непрерывными аспектами планарности заинтересовала математиков и привела к различным характеристикам планарных графов. С точки зрения математики эти характеристики изящны, но эффективных алгоритмов определения планарности они не дают. Наиболее успешный подход к определению планарности состоит просто в том, что граф разбивается на подграфы и затем делается попытка разместить его на плоскости, добавляя подграфы один за другим и сохраняя при размещении планарность.
Вначале сделаем несколько простых, но полезных наблюдений. Поскольку орграф планарен тогда и только тогда, если планарен соответствующий неориентированный граф, полученный игнорированием направления ребер, то достаточно рассматривать только неориентированные графы, поскольку неориентированный граф планарен тогда и только тогда, если все его двусвязные компоненты планарны. Поэтому если неориентированный граф является разделимым, мы можем разложить его на двусвязные компоненты и рассматривать их отдельно. Наконец, поскольку параллельные ребра и петли всегда можно добавить к графу или удалить из него без нарушения свойства планарности, нам достаточно рассматривать только простые графы. Поэтому при определении планарности будем предполагать, что граф неориентированный, простой и двусвязный.
Наша основная стратегия состоит прежде всего в том, чтобы в графе









Представления
Наиболее известный способ представления графа на бумаге состоит в геометрическом изображении точек и линий. В ЭВМ граф должен быть представлен дискретным способом, причем возможно много различных представлений. Простота использования, так же как и эффективность алгоритмов на графе, зависит от подходящего выбора представления графа. Рассмотрим различные структуры данных для представления графов.
Матрица смежностей. Одним из наиболее распространенных машинных представлений простого графа является матрица смежностей или соединений. Матрица смежностей графа








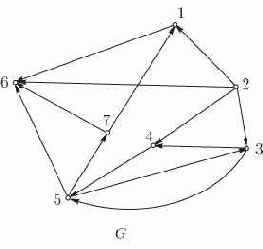
Рис. 12.1. Ориентированный граф и его матрица смежностей

Заметим, что в матрице смежностей петля может быть представлена соответствующим единичным диагональным элементом. Кратные ребра можно представить, позволив элементу матрицы быть больше 1, но это не принято, так как обычно удобно представлять каждый элемент матрицы одним двоичным разрядом.
Для задания матрицы смежностей требуется






Матрица весов. Граф, в котором ребру








Веса несуществующих ребер обычно полагают равными

Список ребер. Если граф является разреженным, то возможно, что более эффектно представлять ребра графа парами вершин. Это представление можно реализовать двумя массивами







Структура смежности. В ориентированном графе вершина













Adj(v) 1: 6 2: 1, 3, 4, 6 3: 4, 5 4: 5 5: 3, 6, 7 6: 7: 1, 6
Если для хранения метки вершины используется одно машинное слово, то структура смежности ориентированного графа требует


Структуры смежности могут быть удобно реализованы массивом из

Матрица инцидентности -








Связность и расстояние
Говорят, что вершины










Подграф графа







Неориентированный граф








Иногда недостаточно знать, что граф связен; нас может интересовать, насколько "сильно связен" связный граф. Например, связный граф может содержать вершину, удаление которой вместе с инцидентными ей ребрами разъединяет оставшиеся вершины. Такая вершина называется точкой сочленения или разделяющей вершиной. Граф, содержащий точку сочленения, называется разделимым. Граф без точек сочленения называется двусвязным или неразделимым. Максимальный двусвязный подграф графа называется двусвязной компонентой или блоком.
Большинство основных вопросов о графах касается связности, путей и расстояний. Нас может интересовать вопрос, является ли граф связным; если он связен, то может оказаться нужным найти кратчайшее расстояние между выделенной парой вершин или определить кратчайший путь между ними. Если граф несвязен, то может потребоваться найти все его компоненты. В нашем курсе строятся алгоритмы для решения этих и других подобных вопросов.
Множество самых разнообразных задач естественно
Множество самых разнообразных задач естественно формулируется в терминах графов. Так, например, могут быть сформулированы задачи составления расписаний в исследовании операций, анализа сетей в электротехнике, установления структуры молекул в органической химии, сегментации программ в программировании, анализа цепей Маркова в теории вероятностей. В задачах, возникающих в реальной жизни, соответствующие графы часто оказываются так велики, что их анализ неосуществим без ЭВМ. Таким образом, решение прикладных задач с использованием теории графов возможно в той мере, в какой возможна обработка больших графов на ЭВМ, и поэтому эффективные алгоритмы решения задач теории графов имеют большое практическое значение. В 16 и 17 лекциях мы излагаем несколько эффективных алгоритмов на графах и используем их для демонстрации некоторой общей техники решения задач на графах с помощью ЭВМ.
Конечный граф
















Бинарный поиск
Когда ячейки таблицы последовательно распределены в памяти с произвольным доступом и имена хранятся в таблице в их естественном порядке, возможен бинарный поиск - один из наиболее широко используемых методов поиска. Идея этого метода состоит в том, чтобы искать имя







Для получения логарифмического времени поиска существенно устанавливать указатель








Бинарный поиск по идее прост, но с деталями условия завершения поиска нужно обращаться осторожно. Частные случаи




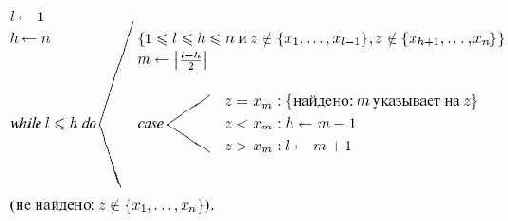
Алгоритм 13.4. Бинарный поиск имени


Корректность алгоритма 13.4 следует из утверждения, данного в комментарии в начале тела цикла. Он устанавливает, что если

находится где-либо в таблице, то оно должно находиться в интервале




Это утверждение очевидно первый раз,
Это утверждение очевидно первый раз, когда мы входим в цикл при






Логарифмический поиск в динамических таблицах
Здесь мы рассмотрим организацию в виде деревьев для таблиц, в которых часто встречаются включения и исключения. Что происходит с временем поиска в дереве, которое модифицировалось путем включения и исключения? Если включенные и исключенные имена выбраны случайно, то оказывается, что в среднем время поиска мало изменяется; но в худшем случае поведение плохое - деревья могут вырождаться в линейные списки, поиск в которых нужно осуществлять последовательно. Проблема вырождения дерева в линейный список, приводящая к времени поиска


Случайные деревья бинарного поиска. Как ведут себя деревья бинарного поиска без ограничений в качестве динамических деревьев? Другими словами, предположим, что дерево бинарного поиска меняется при случайных включениях и исключениях.
Для включения















Алгоритм 13.6. Включение в дерево бинарного поиска
Исключение гораздо сложнее включения, и мы изложим здесь только основную идею. Если подлежащее удалению имя




Вместо этого мы находим в таблице либо имя









Логарифмический поиск в статических таблицах
Мы говорим о логарифмическом времени поиска, как только возникает возможность за время



имен, к задаче поиска в таблице, содержащей не более





решение, которого имеет вид

где



до

Самыми распространенными предположениями, которые дают возможность уменьшить размер таблицы от


за время, не зависящее от






В этом разделе мы рассматриваем только статические таблицы, то есть таблицы, в которых включение и исключение либо не встречаются, либо так редки, что когда они появляются, строится новая таблица. Динамические структуры таблиц, допускающие логарифмическое время поиска, так же как и эффективные алгоритмы включения и исключения, обсуждаются в конце этой лекции. Для статических таблиц нужно обсудить лишь алгоритмы поиска и построения таблицы. Алгоритмы поиска достаточно просты, но некоторые из алгоритмов построения таблицы сложны. Такая ситуация возникает потому, что в случае статической таблицы разумно считать частоты обращения известными, и, может быть, стоит затратить существенные усилия на построение оптимальной таблицы – таблицы с минимальным средним временем поиска (относительно данных частот обращения). Алгоритмы построения таблиц и их анализ являются наиболее важными темами этого раздела.
Оптимальные деревья бинарного поиска
Бинарный поиск в последовательно распределенной таблице ( алгоритм 13.4.) обеспечивает очень быстрое нахождение имен, которые являются средними точками на раннем этапе процесса деления пополам, именно имен, близких к вершине дерева


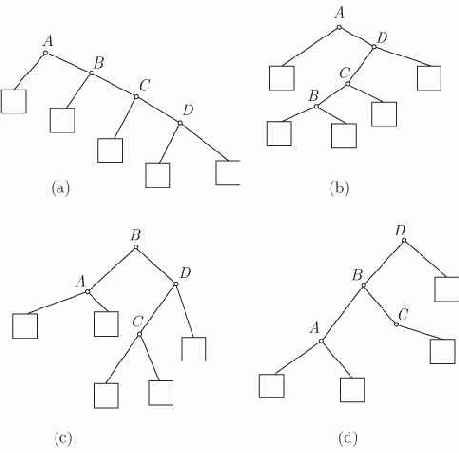
Рис. 13.1. Четыре дерева бинарного поиска над множеством имен {A,B,C,D}
На практике в большинстве таблиц встречаются имена, к которым обращаются гораздо чаще, чем к другим, и "привилегированные" места в таблице разумно постараться использовать для наиболее часто вызываемых имен, а не для имен, выбранных для этих мест в результате бинарного поиска. Это невозможно осуществить для последовательно распределенных таблиц, поскольку место имени определяется его положением относительно естественного порядка имен в таблице. Введем структуру данных, легко приспосабливаемую как к месту бинарного поиска, так и к возможности выделять точки, в которых таблица делится на две части.
Деревом бинарного поиска над именами

называется расширенное бинарное дерево, все внутренние узлы которого помечены различными именами из списка



Поиск имени


Если корня нет (дерево пусто), то




Пусть бинарное дерево имеет вид, в котором каждый узел представляет собой тройку (LEFT, NAME, RIGHT), где LEFT и RIGHTсодержат указатели левого и правого сыновей соответственно, и NAME содержит имя, хранящееся в узле.
Указатели могут иметь значение


Эта процедура нахождения имени


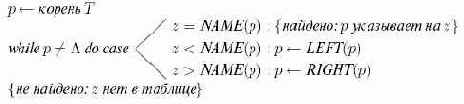
Алгоритм 13.5. Поиск в дереве бинарного поиска
Поиск и другие операции над таблицами
Любой способ поиска оперирует с элементами, которые будем называть именами, взятыми из множества имен


Предположение 1. На

Любые два элемента














Предположение 2. Каждое имя в









Предположение 3. Имеется функция





при отображении



Как уже было отмечено, поиск производится не в самом пространстве





Табличный порядок часто совпадает с естественным порядком, определенным на пространстве имен, однако такое совпадение не обязательно.
Мощность таблицы



Представление о таблице как об упорядоченном множестве имен существенно для многих целей. Но иногда бывает необходимо рассматривать таблицу как множество ячеек, каждая из которых может содержать одно имя. Например, если процесс включения нового имени рассматривать более подробно, то обнаружится, что сначала нужно расширить таблицу добавлением ячейки, для того чтобы заготовить место для новой записи: только потом туда заносится новое имя.
Мы будем предполагать, что имена появляются в таблице не больше одного раза (исключение составляет переходный период, в течение которого заносится новое имя; в таблице допускается два вхождения одного имени). В большинстве случаев вследствие такого предположения таблица с


Существует ряд синонимов для объектов, именуемых здесь таблицей и именем. В обработке данных существуют файлы, элементами которых являются записи; каждая запись есть последовательность полей, одно из которых (участвующее в поиске) называется ключом. Если сам файл проходится во время поиска, "файл" и "ключ" представляют собой то, что мы называем "таблицей" и "именем" соответственно. (Эта терминология несколько двусмысленна, поскольку понятие "ключ" можно отнести либо к самой ячейке, либо к содержимому ячейки.) Однако при поиске в большом файле часто не подразумевается просмотр самого файла; вместо этого поиск осуществляется на справочнике или указателе файла. При успешном поиске найденная в указателе отдельная запись указывает на соответствующую запись в файле.
В таком типе организации файлов нашему понятию таблицы соответствует указатель или справочник.
Мы рассматриваем только четыре табличные операции: поиск, включение, исключение и распечатка. Подробное определение того, что должны делать эти операции над таблицей

поиск





включение


Включение в общем случае предполагает прежде всего поиск соответствующего места, поэтому иногда удобно разделить операцию на две фазы. Сначала используем процедуру поиска для отыскания места, куда должно быть помещено

включить





исключить


Как и включение, исключение иногда реализуется процедурой поиска для получения места

исключить с





Таблица, в которой осуществляются включения или исключения, называется динамической; в противном случае она носит название статической.
Последней операцией, которую мы будем рассматривать для каждой табличной структуры, является
распечатка: & напечатать все имена из

Среди всех операций, которые можно производить над таблицами, четыре, рассматриваемые в этой лекции (поиск, включение, исключение и распечатка), и сортировка (лекции 14, 15) - наиболее важные.
Последовательный поиск
Под последовательным поиском мы подразумеваем исследование имен в том порядке, в котором они встречаются в таблице. При таком поиске в таблице в худшем случае получается просмотр всей таблицы; даже в среднем последовательный поиск имеет тенденцию к использованию числа операций, пропорционального

Для последовательного поиска по таблице


























Алгоритм 13.1. Последовательный поиск














Рассмотрим некоторые аспекты эффективности последовательного поиска, начиная со стандартных методов программирования.
В программе, построенной в виде одного цикла, как алгоритм 13.1, любое значительное ускорение должно быть следствием улучшения кода в цикле. Для того чтобы увидеть, какие операции выполняются внутри цикла, необходимо переписать алгоритм 13.1 в форме, близкой к языку машины:
i


За каждую итерацию выполняется до четырех команд: два сравнения, одна операция увеличения и одна передача управления.
Для ускорения внутреннего цикла общим приемом является добавление в таблицу специальных строк, которые делают необязательной явную проверку того, достиг ли указатель границ таблицы. Это можно сделать в алгоритме 13.1. Если перед поиском мы добавим искомое имя






i




Алгоритм 13.2. Улучшенный последовательный поиск
Улучшение алгоритма 13.1 будет наиболее очевидным, если мы перепишем алгоритм 13.2 в тех же близких к языку машины обозначениях, которые использовались раньше:




При каждой итерации выполняются лишь три действия вместо четырех, как это было в алгоритме 13.1. Таким образом, в большинстве вычислительных устройств цикл в алгоритме 13.2 будет выполняться гораздо быстрее, чем в алгоритме 13.1, и поскольку скорость цикла определяет скорость всей программы, такое же сравнение имеет место для двух программ.
Печально то, что фокус с добавлением

Единственным недостатком алгоритма 13. 2 является то, что при безуспешном поиске (поиске имен, которых нет в таблице) всегда просматривается вся таблица. Если такой поиск возникает часто, то имена надо хранить в естественном порядке; это позволяет завершать поиск, как только при просмотре попалось первое имя, большее или равное аргументу поиска. В этом случае в конец таблицы следует добавить фиктивное имя




i


Алгоритм 13.3.Последовательный поиск по таблице, хранимой в естественном порядке
Сбалансированные сильно ветвящиеся деревья
Деревья бинарного поиска естественным образом обобщаются до


сыновей и содержит



поддеревьев узла. На рис. 13.2 показано полностью заполненное 5-арное дерево с двумя уровнями. Заметим, что мы не можем требовать, чтобы каждый узел










Как и в деревьях бинарного поиска, полезно различать внутренние узлы и листья. Внутренний узел содержит


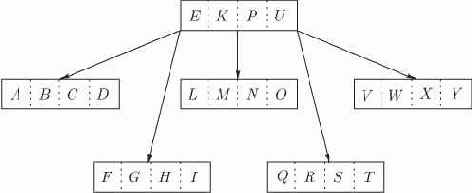
Рис. 13.2. Абсолютно сбалансированное, полностью заполненное 5-арное дерево поиска
Сбалансированное сильно ветвящееся дерево порядка


Все листья расположены на одном уровне.Корень имеет





в комбинаторных алгоритмах, так как
Задача поиска является фундаментальной в комбинаторных алгоритмах, так как она формулируется в такой общности, что включает в себя множество задач, представляющих практический интерес. При самой общей постановке "Исследовать множество








Обменная сортировка
Обменная сортировка некоторым систематическим образом меняет местами пары имен, не отвечающие порядку, до тех пор, пока такие пары существуют. Фактически алгоритм 14.1 можно рассматривать как обменную сортировку, в которой имя

Пузырьковая сортировка. Наиболее очевидный метод систематического обмена местами имен с неправильным порядком состоит в просмотре пар смежных имен последовательно слева направо и перемене мест тех имен, которые не отвечают порядку.
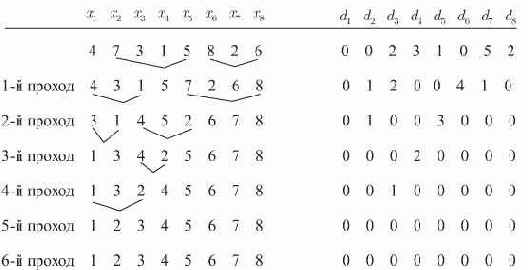
Рис. 14.2. Пузырьковая сортировка, примененная к таблице. Показан вектор инверсии таблицы после каждого прохода
Эта техника получила название пузырьковой сортировки, так как большие имена "пузырьками всплывают" вверх (то есть на правый конец) таблицы. В алгоритме 14.2 эта простая идея реализуется с одним небольшим усовершенствованием: ясно, что не имеет смысла продолжать просмотр для больших имен (в правом конце таблицы), про которые известно, что они находятся на своих окончательных позициях. В алгоритме 14.2 используется переменная


равно наибольшему индексу



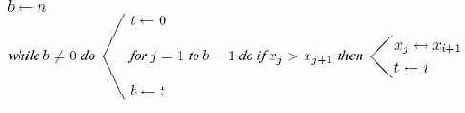
Алгоритм 14.2. Пузырьковая сортировка
Анализ пузырьковой сортировки зависит от трех факторов: числа проходов (то есть числа выполнений тела цикла





дает возможность предположить, что каждый проход пузырьковой сортировки, исключая последний, уменьшает на единицу каждый ненулевой элемент вектора инверсий и циклически сдвигает вектор на одну позицию влево; легко доказать, что это верно в общем случае, и поэтому число проходов равно единице плюс наибольший элемент вектора инверсий. В лучшем случае имеется всего один проход, в худшем случае -








Пузырьковую сортировку можно несколько улучшить, но при этом она все еще не сможет конкурировать с более эффективными алгоритмами сортировки. Ее единственным преимуществом является простота.
Как в простой сортировке вставками, так и в пузырьковой сортировке (алгоритм 14.2) основной причиной неэффективности является тот факт, что обмены дают слишком малый эффект, так как в каждый момент времени имена сдвигаются только на одну позицию. Такие алгоритмы непременно требуют порядка

операций, как в среднем, так и в худшем случаях.
Быстрая сортировка. Идея метода быстрой сортировки состоит в том, чтобы выбрать одно из имен в таблице и использовать его для разделения таблицы на две подтаблицы, составленные соответственно из имен меньших и больших выбранного, которые затем рекурсивно сортируются с использованием быстрой сортировки. Разделение можно реализовать, одновременно просматривая таблицу и слева направо, и справа налево, меняя местами имена в неправильных частях таблицы. Имя, используемое для расщепления таблицы, затем помещается между двумя подтаблицами, и две подтаблицы сортируются рекурсивно.
В алгоритме 14.3 показаны детали быстрой сортировки для сортировки таблицы


используется для разбиения таблицы на подтаблицы. На рис. 14.3 показано, как алгоритм 14.3 использует два указателя







встречаются, то есть когда






Алгоритм 14.3. Рекурсивный вариант быстрой сортировки, использующий первое имя для расщепления таблицы. Предполагается, что имя

определено и больше или равно


Рис. 14.3. Фаза разбиения быстрой сортировки, использующей первое имя для разбиения таблицы. Значение

Алгоритм 14.3 изящен, но непрактичен. Проблема состоит в том, что рекурсия используется для записи подтаблиц, которые рассматриваются на более поздних этапах, и в худших случаях (когда таблица уже отсортирована) глубина рекурсии может равняться







увеличить изображение
Алгоритм 14.4.Итерационный вариант быстрой сортировки

Внутренняя сортировка
Существует по крайней мере пять широких классов алгоритмов внутренней сортировки.
Вставка. На



уже отсортированным именами:

Обмен. Два имени, расположение которых не соответствует порядку, меняются местами (обмен). Эти процедуры повторяются до тех пор, пока остаются такие пары.

Выбор. На



Распределение. Имена распределяются по группам, и содержимое групп затем объединяется таким образом, чтобы частично отсортировать таблицу; процесс повторяется до тех пор, пока таблица не будет отсортирована полностью.Слияние. Таблица делится на подтаблицы, которые сортируются по отдельности и затем сливаются в одну.
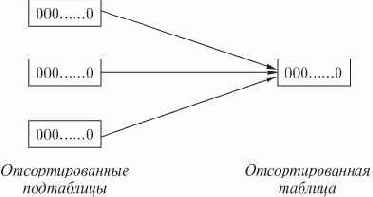
Эти классы нельзя назвать ни взаимоисключающими, ни исчерпывающими: одни алгоритмы сортировки можно с полным основанием отнести более чем к одному классу (пузырьковую сортировку можно рассматривать и как выбор, и как обмен), а другие не укладываются ни в один из классов. Тем не менее, перечисленные пять классов достаточно удобны для классификации обсуждаемых алгоритмов сортировки.
Сосредоточим внимание на первых четырех классах алгоритмов сортировки. Алгоритмы, основанные на слиянии, приемлемы для внутренней сортировки, но более естественно рассматривать их как методы внешней сортировки.
В описываемых алгоритмах сортировки имена образуют последовательность, которую будем обозначать
















Таким образом, операция

Однако это условие всегда обязательно восстанавливается.
В каждом из рассматриваемых алгоритмов будем считать, что имена нужно сортировать на месте. Другими словами, переразмещение имен должно происходить внутри последовательности


Вставка
Вставка - простейшая сортировка вставками проходит через этапы



вставляется на свое правильное место среди

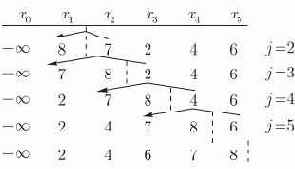
Рис. 14.1. Простая сортировка вставками, используемая на таблице из n = 5 имен. Пунктирные вертикальные линии разделяют уже отсортированную часть таблицы и еще не отсортированную
При вставке имя







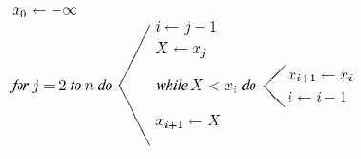
Алгоритм 14.1. Простая сортировка вставками
Эффективность этого алгоритма, как и большинства алгоритмов сортировки, зависит от числа сравнений имен и числа пересылок данных, осуществляемых в трех случаях : худшем, среднем (в предположении, что все

Рассматриваемые здесь задачи можно отнести
Рассматриваемые здесь задачи можно отнести к наиболее часто встречающимся классам комбинаторных задач. Почти во всех машинных приложениях множество объектов должно быть переразмещено в соответствии с некоторым заранее определенным порядком. Например, при обработке коммерческих данных часто бывает необходимо расположить их по алфавиту или по возрастанию номеров. В числовых расчетах иногда требуется знать наибольший корень многочлена, и т.д.
Будем считать заданной таблицу с











для которой






При внутренней сортировке решается задача полной сортировки для случая достаточно малой таблицы, умещающейся непосредственно в адресной памяти. Внешняя сортировка представляет собой задачу полной сортировки для случая такой большой таблицы, что доступ к ней организован по частям, расположенным на внешних запоминающих устройствах. Частичная сортировка - задачи выбора

Частичная сортировка
Ранее мы изучали проблему полного упорядочения множества имен, не имея a priori информации об абстрактном порядке имен. Имеется два очевидных уточнения этой проблемы. Вместо полного упорядочения требуется только определить


Частичная сортировка (слияние)
Вторым направлением исследования частичной сортировки является задача слияния двух отсортированных таблиц


в одну отсортированную таблицу





Алгоритм 15.5. Прямое слияние

Частичная сортировка (выбор)
Как при данных именах









Конечно, все перечисленные варианты задачи выбора можно решить, используя любой из методов полной сортировки имен и затем тривиально обращаясь к



При использовании алгоритма сортировки для выбора наиболее подходящим будет один из алгоритмов, основанных на выборе: либо простая сортировка выбором (алгоритм 15.1) либо пирамидальная сортировка (алгоритм 15.3). В каждом случае мы можем остановиться после того, как выполнены первые


сравнений имен, а для пирамидальной — использование


Цифровая распределяющая сортировка
Цифровая распределяющая сортировка основана на наблюдении, что если имена уже отсортированы по младшим разрядами









Использовать поля связи



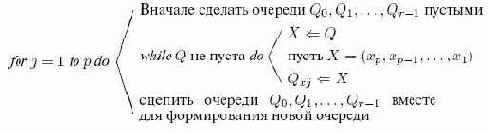
Алгоритм 15.4.Цифровая распределяющая сортировка
Распределяющая сортировка
Обсуждаемый здесь алгоритм сортировки отличается от рассматривавшихся до сих пор тем, что он основан не на сравнениях между именами, а на представлении имен. Мы полагаем, что каждое из имен


и их нужно отсортировать в возрастающем лексикографическом порядке, то есть

тогда и только тогда, если для некоторого

имеем







Внешняя сортировка
В методах сортировки, обсуждавшихся в предыдущем разделе, мы полагали, что таблица умещается в быстродействующей внутренней памяти. Хотя для большинства реальных задач обработки данных это предположение слишком сильно, оно, как правило, выполняется для комбинаторных алгоритмов. Сортировка обычно используется только для некоторого сокращения времени работы алгоритмов, в которых сортировка применяется только для некоторого сокращения времени работы алгоритмов, когда оно недопустимо велико даже для задач "умеренных" размеров. Например, часто бывает необходимо сортировать отдельные предметы во времени исчерпывающего поиска (лекция 13), но поскольку такой поиск обычно требует экспоненциального времени, маловероятно, что подлежащая сортировке таблица будет настолько большой, чтобы потребовалось использование запоминающих устройств. Однако задача сортировки таблицы, которая слишком велика для основной памяти, служит хорошей иллюстрацией работы с данными большого объема, и поэтому в этом разделе мы обсудим важные идеи внешней сортировки. Более того, будем рассматривать только сортировку таблицы путем использования вспомогательной памяти с последовательным доступом. Условимся называть эту память лентой.
Общей стратегией в такой внешней сортировке является использование внутренней памяти для сортировки имен из ленты по частям так, чтобы производить исходные отрезки (известные также как цепочки) имен в возрастающем порядке. По мере порождения эти отрезки распределяются по

рабочим лентам, и затем производится их слияние по





Самый очевидный метод для получения исходных отрезков состоит в том, что можно просто считывать


Все полученные таким образом исходные отрезки содержат


Порождение исходных отрезков продолжается следующим образом. Из входной ленты считываются первые

Разумный путь реализации этой процедуры состоит в том, чтобы рассматривать каждое имя





Порождает ли этот выбор с замещением длинные отрезки? Ясно, что он делает это, по крайней мере, не хуже, чем очевидный метод, так как все отрезки (кроме, возможно, последнего) содержат не меньше



После того, как порождены исходные отрезки, возникает задача повторного распределения их по рабочим лентам и слияния их вместе до тех пор, пока в конце концов мы не получим окончательную отсортированную таблицу. Простейший метод состоит в том, чтобы распределить отрезки по лентам

равномерно и произвести их слияние на ленту




Выбор
В сортировке посредством выбора основная идея состоит в том, чтобы идти по шагам





имен. Число сравнений имен на



независимо от входа, поэтому ясно, что это не очень хороший способ сортировки.
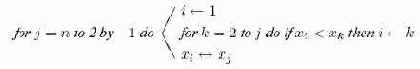
Алгоритм 15.1. Простая сортировка выбором
Несмотря на неэффективность алгоритма 15.1, идея выбора может привести и к эффективному алгоритму сортировки. Весь вопрос в том, чтобы найти более эффективный метод определения



Заметим, что для определения наибольшего имени этот процесс требует


Идея турнира с выбыванием прослеживается при сортировке весьма отчетливо, если имена образуют пирамиду. Пирамида - это полностью сбалансированное бинарное дерево высоты






Таким образом, пирамида, представленная на рисунке 15.3, принимает вид

Заметим, что в пирамиде наибольшее имя должно находиться в корне и, таким образом, всегда в первой позиции массива, представляющего пирамиду. Обмен местами первого имени с




Это общее описание пирамидальной сортировки.
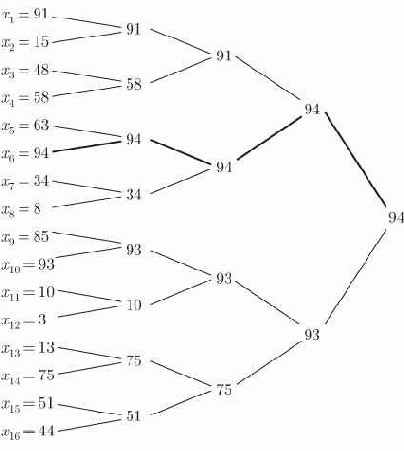
Рис. 15.1. Использование турнира с выбыванием для отыскания наибольшего имени.Путь наибольшего имени показан жирной линией
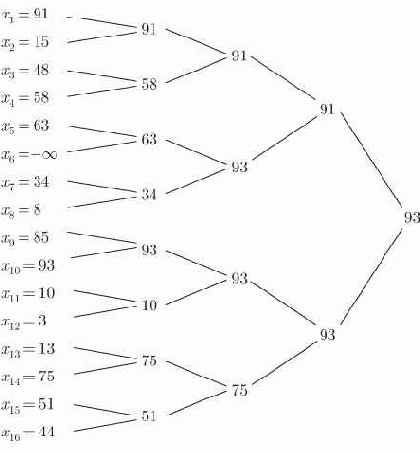
Рис. 15.2. Отыскание второго наибольшего имени путем замены наибольшего имени на

Процедура RESTORE


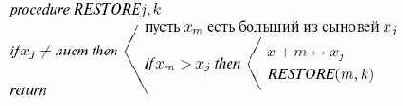
Переписывая это итеративным способом и дополняя деталями, мы получим алгоритм 15.2.
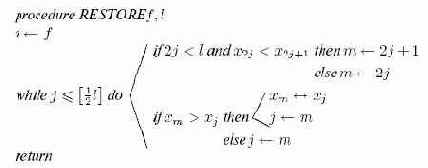
Алгоритм 15.2.Восстановление пирамиды из дерева, поддеревья которого суть пирамиды
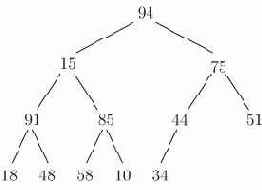
Рис. 15.3. Пирамида, содержащая 12 имен
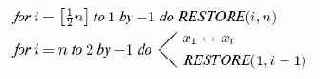
Алгоритм 15.3.Пирамидальная сортировка
Алгоритм Дейкстры нахождения кратчайшего пути
Рассмотрим алгоритм нахождения путей в ориентированном графе. Пусть есть ориентированный граф


Можно представить орграф







Для решения поставленной задачи будем использовать "жадный" алгоритм, который называют алгоритмом Дейкстры (Dijkstra). Алгоритм строит множество






Алгоритм Флойда нахождения кратчайших путей между парами вершин
Предположим, что мы имеем помеченный орграф, который содержит время полета по маршрутам, связывающим определенные города, и~мы хотим построить таблицу, где приводилось бы минимальное время перелета из одного (произвольного) города в любой другой. В этом случае мы сталкиваемся с общей задачей нахождения кратчайших путей, то есть нахождения кратчайших путей между всеми парами вершин орграфа.
Формулировка задачи.Есть ориентированный граф








Можно решать эту задачу, последовательно применяя алгоритм Дейкстры для каждой вершины, объявляемой в качестве источника. Но мы для решения поставленной задачи воспользуемся алгоритмом, предложенным Флойдом (R.W. Floyd). Пусть все вершины орграфа последовательно пронумерованы от 1 до








в вершину

Над матрицей







Вычисление на


Верхний индекс


после

Для вычисления













изменяется. Рассмотрим орграф:
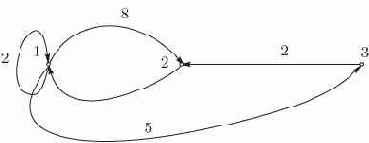
Рис. 16.1. Помеченный орграф
Матрица A(3 * 3) на нулевой итерации (k = 0)

Матрица A(3 * 3) после первой итерации (k = 1)

Матрица A(3 * 3) после второй итерации (k = 2)

Матрица A(3 * 3) после третьей итерации (k = 3)

Поиск в глубину
При решении многих задач, касающихся ориентированных графов, необходим эффективный метод систематического обхода вершин и дуг орграфов. Таким методом является метод поиск в глубину. Метод поиска в глубину является основой многих эффективных алгоритмов работы с графами. Предположим, что есть ориентированный граф









Метод получил свое название - поиск в глубину, поскольку поиск не посещенных вершин идет в направлении вглубь до тех пор, пока это возможно. Например, пусть




помечена меткой "


помечена меткой "










Программы
Программа 1. Построение матрицы инциндентности.
//Построение матрицы инциндентности //Программа реализована на языке программирования Turbo-C++
\begin{verbatim} #include <stdio.h> #include <stdlib.h> #include <string.h> #include <conio.h> #include <iostream.h>
struct elem { int num; /* Номер вершины */ int suns; /* Количество сыновей */ char str[20]; /* Строка с номерами сыновей */ elem *next; /* Указатель на следующую вершину */ } *head, *w1, *w2;
int Connected(int i, int j) { int k; char *str1; w2 = head; if(i == j) return 0; for(k=1; k<i; k++) w2 = w2->next; if( strchr(w2->str, j) ) return 1; return 0; }
void main() {
int tops; int i,j,k,l; char *str1;
clrscr(); printf("Введите количество вершин \n"); scanf("%d", &tops);
head = (elem *)malloc(sizeof(elem)); head->num = 1; head->suns = 0; head->str[0] = '\0'; head->next = NULL;
w1 = head;
for(i=2;i<=tops;i++) { w2 = (elem *)malloc(sizeof(elem)); w2->num = i; w2->suns = 0; w2->str[0] = '\0'; w2->next = NULL;
w1->next = w2; w1 = w2; }
w1 = head;
for(i=1; i<=tops; i++) { // clrscr(); printf("Введите количество путей из вершины %d\n", i); scanf("%d", &k);
for(j=1; j<=k; j++) { printf("Введите связь %d\n", j); scanf("%d", &l); if((l<=0) || (l > tops)) { printf("Такой вершины нет, повторите попытку\n"); l = 0; j--; continue; } w1->str[w1->suns++] = l; w1->str[w1->suns] = '\0'; if(w1->suns == 49) { printf("Слишком много связей !"); exit(1); } } w1 = w1->next; } clrscr(); printf("\n\n Матрица инциндентности :\n"); for(i=1; i<=tops; i++) { printf("\n %d) ", i); for(j=1; j<=tops; j++) { printf("%d ", Connected(i, j)); } } printf("\n\n Нажмите любую клавишу\ldots "); getch(); }
Программа 2.Поиск вершин, недостижимых из заданной вершины графа.
//Поиск вершин, недостижимых из заданной вершины графа. //Программа реализована на языке программирования Turbo-C++
\begin{verbatim} #include <iostream.h> #include <fstream.h> //- - - - - - - - - - - - - - - - - - - - - - int n,s; int c[20][20]; int r[20]; //- - - - - - - - - - - - - - - - - - - - - - int load(); int save(); int solve(); //- - - - - - - - - - - - - - - - - - - - - - int main(){ load(); solve(); save(); return 0; } //- - - - - - - - - - - - - - - - - - - - - - int load(){ int i,j; ifstream in("input.txt"); in"n"s; s--; for (i=0; i<n; i++) for (j=0; j<n; j++) in"c[i][j]; in.close(); return 0; }
int save(){ int i; ofstream out("output.txt"); for (i=0; i<n; i++) if (r[i]==0) out"i+1"" "; out.close(); return 0; } //- - - - - - - - - - - - - - - - - - - - - - int solve(){ int i,h,t; int q[400]; for (i=0; i<n+1; i++) q[i]=0; r[s]=1; h=0; t=1; q[0]=s; while (h<t){ for (i=0;i<n;i++) if ((c[q[h]][i]>0)&(r[i]==0)){ q[t]=i; t++; r[i]=1; } h++; } return 0; }
Программа 3. Поиск циклов в графе.
{> Реализация на Turbo-Pascal. Поиск циклов в графе <}
{$R-,I-,S-,Q-}
const MAXN = 40; QUERYSIZE = 600;
type vert = record x: integer; s: array [1..MAXN] of integer; end;
var c : array [1..MAXN,1..MAXN] of integer; n : integer;
wr : vert;
res : array [1..MAXN] of string; resv: integer; ss : string;
procedure load; var i,j: integer; begin assign(input,'input.txt'); reset(input); read(n); for i:=1 to n do for j:=1 to n do read(c[i][j]); close(input); end;
function saveway(i:integer):string; var e:string; begin str(i,e); if (wr.s[i]=-1) then saveway:=e+' ' else saveway:=saveway(wr.s[i])+e+' '; end;
p>function findss(s: string): boolean; var i : integer; l1,l2,rs : string; i1,i2,i22 : integer;
begin findss:=false; l2:=copy(s,1,pos(' ',s)-1); i2:=length(l2); i22:=length(s); for i:=1 to resv do begin l1:=copy(res[i],1,pos(' ',res[i])-1); i1:=length(l1); rs:=copy(res[i],1,length(res[i])-i1)+res[i]; if (length(res[i])+i2=i22+i1)and(pos(s,rs)>0) then begin findss:=true; exit; end; end; end;
procedure solve; var h,t,i,j: integer; q : array [1..QUERYSIZE] of vert; e : string; begin resv:=0; fillchar(res,sizeof(res),0);
for i:=1 to n do begin fillchar(q[i],sizeof(q[i]),0); q[i].x:=i; q[i].s[i]:=-1; end;
t:=n+1; h:=1; while h<t do begin for i:=1 to n do if (c[q[h].x,i]>0) then begin if (q[h].s[i]=-1) then begin wr:=q[h]; str(i,e); ss:=saveway(q[h].x)+e; if (not findss(ss)) then begin inc(resv); res[resv]:=ss; end; end; if (q[h].s[i]=0) then begin q[t]:=q[h]; q[t].x:=i; q[t].s[i]:=q[h].x; inc(t); end; end; inc(h); end;
close(output); end;
procedure save; var i: integer; begin assign(output,'output.txt'); rewrite(output); for i:=1 to resv do writeln(res[i]); close(output); end;
begin load; solve; save; end.

Автоматическое построение лабиринтов
Тезей должен был найти выход из Критского лабиринта или погибнуть, убитый Минотавром. Но что поразительно: найти вход в лабиринт - задача не менее трудная.
Здесь не представляется возможным описать все мыслимые лабиринты, да это и не требуется. Мы займемся простыми лабиринтами, построенными на прямоугольнике




Рис. 17.1. Пример лабиринта
Один из возможных подходов к решению таков. Выбираем вход; затем, начав от него, добавляем по одной ячейке к главному пути-решению, пока он не достигнет выходной стороны. После этого удаляем некоторые внутренние стенки так, чтобы все клетки оказались соединенными с главным путем. Чтобы главный путь не получился прямым коридором, следует при его построении предусмотреть случайные повороты. Программа должна также следить за тем, чтобы при построении главного пути или при открытии боковых ячеек не нарушалась единственность решения. Наблюдательный читатель заметит, что определение единственности решения не годится в случае, когда путь заходит в боковой тупик и затем возвращается.
Программу можно написать почти на любом из процедурных языков.
Программа 1. Лабиринт.
{Программно задаются вход и выход. Нажимая на клавишу "Enter", перебираем всевозможные пути от входа до выхода в лабиринте. Выход из программы по клавише "Esc". Алгоритм реализован на языке программирования Turbo-Pascal}
program Maze; uses Graph, Crt;
var m,n: Integer; Matrix: array [1..100,1..100] of Boolean; Start,Finish: Integer;
procedure PrepareGraph; var Driver,Mode: Integer; begin Driver:=VGA; Mode:=VGAHi; InitGraph(Driver,Mode,'c:\borland\tp\bgi'); end;
procedure DisplayMaze(x1,y1,x2,y2: Integer); var i,j: Integer; dx,dy: Real; begin SetFillStyle(1,8); SetColor(15); dx:=(x2-x1)/m; dy:=(y2-y1)/n; for i:=1 to n do for j:=1 to m do if not Matrix[i,j] then Rectangle(Round(x1+(i-1)*dx),Round(y1+(j-1)*dy), Round(x1+i*dx),Round(y1+j*dy)); end;
function CreatesPath(i,j: Integer): Boolean; var Result: Boolean; Count: Integer; ii,jj: Integer; begin Count:=0; if (i>1) and Matrix[i-1,j] then Inc(Count); if (i<m) and Matrix[i+1,j] then Inc(Count); if (j>1) and Matrix[i,j-1] then Inc(Count); if (j<m) and Matrix[i,j+1] then Inc(Count); if Count>1 then Result:=true else Result:=false; CreatesPath:=Result; end;
function DeadEnd(i,j: Integer): Boolean; var Result: Boolean; Count: Integer; begin Count:=0; if (i=2) or CreatesPath(i-1,j) then Inc(Count); if (i=m-1) or CreatesPath(i+1,j) then Inc(Count); if (j=2) or CreatesPath(i,j-1) then Inc(Count); if (j=n-1) or CreatesPath(i,j+1) then Inc(Count); if Count=4 then Result:=true else Result:=false; DeadEnd:=Result; end;
function CreateMaze: Boolean; var i,j: Integer; di,dj: Integer; Result: Boolean; begin Randomize; for i:=1 to n do for j:=1 to m do Matrix[i,j]:=false; Start:=Random(m-2)+2; i:=Start; j:=2; Matrix[Start,1]:=true; repeat Matrix[i,j]:=true; di:=0; dj:=0; while (di=0) and (dj=0) do begin di:=1-Random(3); if (i+di=1) or (i+di=m) then di:=0; if di=0 then dj:=1-Random(3); if j+dj=1 then dj:=0; if CreatesPath(i+di,j+dj) then begin di:=0; dj:=0; end; end; i:=i+di; j:=j+dj; until DeadEnd(i,j) or (j=n); Finish:=i; Matrix[Finish,n]:=true; if j<n then Result:=false else Result:=true; CreateMaze:=Result; end;
begin m:=6; n:=6;
PrepareGraph; repeat ClearDevice; repeat until CreateMaze; DisplayMaze(120,40,520,440); repeat until KeyPressed; until ReadKey=#27; CloseGraph; end.
Программа 2. Лабиринт.
{ Лабиринт реализуется автоматически, без участия пользователя. Алгоритм реализован на языке программирования Turbo-Pascal } uses graph,crt; var mpos,npos,m,n,delx,x,y,t,gd,gm,i,k:integer;
begin randomize; writeln('Input labyrint size (x and y)'); readln(m,n); writeln('Input entrance&exit coordinates (mpos<m and npos<m)'); readln(mpos,npos); initgraph(gd,gm,'c:\borland\tp\bgi'); for i:=1 to m do begin for k:=1 to n do begin rectangle(90+10*i,90+10*k,90+10*i+10,90+10*k+10); end; end; setfillstyle(1,0); setcolor(0); line(100+(mpos-1)*10+1,100,100+(mpos-1)*10+9,100); line(100+(npos-1)*10+1,100+n*10,100+(npos-1)*10+9,100+n*10); y:=n; x:=npos; readln;
while y>1 do begin delx:=random(m)-x+1; if y=2 then delx:=mpos-x; i:=91+x*10; if i<90+(x+delx)*10 then begin while i<>90+(x+delx)*10 do begin i:=i+1; line(i,91+y*10,i,99+y*10); end; end;
if i>91+(x+delx)*10 then begin while i<>91+(x+delx)*10 do begin i:=i-1; line(i,91+y*10,i,99+y*10); end; end;
x:=x+delx; line(91+10*x,90+y*10,99+10*x,90+y*10);
y:=y-1;
end;
readln; end.
Бинарное дерево
Строится бинарное дерево. В узлы дерева засылаются целые положительные числа, выбранные случайным образом. После задания значений вершин на каждом уровне эти значения выводятся на экран, начиная с корневой. Пользователю предлагается сделать выбор номера уровня, в нем определяется максимальное значение и выводится на экран.
Программа 3. Поиск максимального элемента.
{ Алгоритм реализован на языке программирования Turbo-Pascal} uses crt; type sp=^tree; tree=record val:integer; l:sp; r:sp; end; var t:sp; nh, max,h,i:integer; procedure find(t:sp; h,nh:integer); begin if t=nil then exit; if h=nh then begin if t^.val> max then max:=t^.val; end else begin find(t^.l,h+1,nh); find(t^.r,h+1,nh); end; end; procedure zadtree(var t:sp; h,nh:integer); begin if h=5 then begin new(t); t^.l:=nil; t^.r:=nil; t^.val:=random(100); end else begin new(t); zadtree(t^.l, h+1,nh); zadtree(t^.r, h+1,nh); t^.val:=random(100); end; end; procedure writetree(t:sp; h,nh:integer); begin if t=nil then exit; if h=nh then begin write(t^.val,' '); end else begin writetree(t^.l,h+1,nh); writetree(t^.r,h+1,nh); end; end; begin clrscr; randomize; t:=nil; zadtree(t,1,nh); for i:=1 to 5 do begin writetree(t,1,i); writeln; end; max:=0; write('vvedite uroven '); readln(nh); find(t,1,nh); write('max= ',max); readln; end.
Ханойская башня
В лекции 11 дана реализация алгоритма “Ханойская башня”. Здесь используется другой подход. В программе реализован пользовательский интерфейс с развитым эргономическим компонентом. Пользователю предоставляется возможность самому решить поставленную задачу. В программе использована работа с видеостраницами.
Постановка задачи.
На стержне в исходном порядке находится дисков, уменьшающихся по размеру снизу вверх. Диски должны быть переставлены на стержень в исходном порядке при использовании в случае необходимости промежуточного стержня для временного хранения дисков. В процессе перестановки дисков обязательно должны соблюдаться правила: одновременно может быть переставлен только один самый верхний диск (с одного из стержней на другой); ни в какой момент времени диск не может находиться на другом диске меньшего размера.
Программа 12. Ханойская башня.
{Программа реализована с помощью абстрактного типа данных – стек для произвольного числа дисков. Число колец задается константой maxc. Программа написана на языке программирования Turbo-Pascal}
program Tower; uses Crt, Graph;
const maxc = 4;{Максимальное число колец на одной башне}
type TTower = record num: byte; sizes: array[1..maxc] of byte; up: byte; end;
var Towers: array[1..3] of TTower; VisVP, ActVP: byte; {видимая и активная видеостраницы} ActTower: byte; Message: String; Win: boolean; font1: integer;
function CheckEnd: boolean; var res: boolean; i: byte; begin res:=False; if (Towers[2].num=maxc) or (Towers[3].num=maxc) then res:=true; CheckEnd:=res; end;
procedure BeginDraw; begin SetActivePage(ActVP); end;
procedure EndDraw; begin
VisVP:=ActVP; SetVisualPage(VisVP); if VisVP=1 then ActVP:=0 else ActVP:=1; end;
procedure Init; var grDr, grM: integer;
ErrCode: integer; i: integer; begin grDr:=VGA; grM:=VGAMed; InitGraph(grDr, grM, 'c:\borland\tp\bgi'); ErrCode:=GraphResult; if ErrCode <> grOk then begin Writeln('Graphics error:', GraphErrorMsg(ErrCode)); Halt; end;
Towers[1].num:=maxc; Towers[1].up:=0; for i:=0 to maxc-1 do Towers[1].sizes[i+1]:=maxc-i;
Towers[2].num:=0; Towers[2].up:=0; for i:=0 to maxc-1 do Towers[2].sizes[i+1]:=0;
p>Towers[3].num:=0; Towers[3].up:=0; for i:=0 to maxc-1 do Towers[2].sizes[i+1]:=0;
ActTower:=1; VisVP:=0; ActVP:=1; SetVisualPage(VisVP); SetActivePage(ActVP); Message:=''; Win:=False; end;
procedure Close; begin closegraph; end;
procedure DrawTower(x, y: integer; n: integer); var i: integer; begin if n=ActTower then SetColor(yellow); Line(x, y, x, y+15+maxc*15); for i:=1 to Towers[n].num do begin Rectangle(x-10*Towers[n].sizes[i], y+15+15*(maxc-i+1), x+10*Towers[n].sizes[i], y+15+15*(maxc-i)) end;
if Towers[n].up<>0 then begin Rectangle(x-10*Towers[n].up, y-15, x+10*Towers[n].up, y-30); end;
SetColor(White); end;
procedure DrawInfo; begin OutTextXY(50, 20, 'Ханойская башня.); OutTextXY(80, 40, 'Работа с программой: стрелки влево-вправо - выбор башни'); OutTextXY(130, 60, 'текущая башня выделяется желтым цветом'); OutTextXY(60, 80, 'стрелка вверх - поднять кольцо, стрелка вниз - положить кольцо'); OutTextXY(80, 100, '(две последние операции выполняются для активной башни)');
end;
procedure Draw; begin BeginDraw; ClearDevice; OutTextXY(180, 140, Message); Message:=''; DrawTower(150, 200, 1); DrawTower(300, 200, 2); DrawTower(450, 200, 3);
if win then begin SetTextStyle(GothicFont, HorizDir, 8); SetColor(Red); Outtextxy(70, 0, 'Congratulations'); Outtextxy(160, 70, 'You win'); SetTextStyle(DefaultFont, HorizDir, 1); SetColor(White); OutTextXY(250, 330, 'Press any key'); end else DrawInfo; EndDraw; end;
procedure MainCycle; var ch: char; ex: boolean; up: byte; begin ex:=False; repeat if KeyPressed then begin ch:=ReadKey; case ch of #27: begin Ex:=True; end; #77: begin up:=Towers[ActTower].up; Towers[ActTower].up:=0; inc(ActTower); if ActTower>3 then ActTower:=1; Towers[ActTower].up:=up; end; #75: begin up:=Towers[ActTower].up; Towers[ActTower].up:=0; dec(ActTower); if ActTower<1 then ActTower:=3; Towers[ActTower].up:=up; end; #80: begin {вниз} if Towers[ActTower].up<>0 then begin if Towers[ActTower].num=0 then begin Towers[ActTower].num:=Towers[ActTower].num+1;
Towers[ActTower].sizes[Towers[ActTower].num]:=Towers[ActTower].up; Towers[ActTower].up:=0; end else begin if Towers[ActTower].sizes[Towers[ActTower].num]>Towers[ActTower].up then begin Towers[ActTower].num:=Towers[ActTower].num+1;
Towers[ActTower].sizes[Towers[ActTower].num]:=Towers[ActTower].up; Towers[ActTower].up:=0; end else Message:='Это кольцо сюда опускать нельзя'; end; end; end; #72: begin {вверх} if Towers[ActTower].num<>0 then begin Towers[ActTower].num:=Towers[ActTower].num-1;
Towers[ActTower].up:=Towers[ActTower].sizes[Towers[ActTower].num+1]; Towers[ActTower].sizes[Towers[ActTower].num+1]:=0; end; end; end; if CheckEnd then begin Win:=True; ex:=True; end; Draw; end; until ex; end;
begin Init; Draw; MainCycle; if win then repeat until keypressed; Close; end.

Сортировки
В лекциях 14 и 15
мы рассматривали более подробно различные способы сортировки. Здесь мы напоминаем некоторые из них и приводим пример программ.
Сортировка упорядочивает совокупность объектов в соответствии с заданным отношением порядка. Ключ сортировки - поле или группа полей элемента сортировки, которые используются при сравнении во время сортировки. Сортирующая последовательность - схема упорядочивания. Например, можно взять последовательность символов алфавита, задающую способ упорядочения строк этого алфавита.
Способ сортировки: сортировка по возрастанию, сортировки по убыванию. Методы сортировки:
метод прямого выбора;метод пузырька;метод по ключу;сортировки слиянием;сортировки Батчера.
Сортировка по возрастанию - это сортировка, при которой записи упорядочиваются по возрастанию значений ключевых полей.
Сортировка по убыванию - это сортировка, при которой записи упорядочиваются по убыванию значений ключевых полей.
Сортировка методом пузырька (пузырьковая сортировка) - способ сортировки, заключающийся в последовательной перестановке соседних элементов сортируемого массива.
Сортировка по ключу - это сортировка записей с упорядочением по значению указанного поля или группы полей.
Сортировка слиянием - это внешняя сортировка, при которой на первом этапе группы записей сортируются в оперативной памяти и записываются на несколько внешних носителей; на втором этапе упорядоченные группы сливаются с нескольких внешних носителей на один носитель данных. Носитель данных - материальный объект, предназначенный для хранения данных, или среда передачи данных.
Сортировка Батчера - это сортировка, внутренний алгоритм которой работает за время

Программа 5. Сортировка массива по возрастанию методом пузырька.
//Данные, которые нужно отсортировать, берутся из файла "massiv.txt", //результат записывается в массив int mas['K'] и выводится на экран // Алгоритм реализован на Turbo C++. #include <conio.h> #include <stdio.h> #define K 1000; //Размер массива
int mas['K']; int n; void puzirek()// функция сортирует массив по возрастанию методом пузырька { int i,j,t; for(i=0;i<n;i++) for(j=1;j<n-i;j++) if(mas[j]<mas[j-1]) { t=mas[j]; mas[j]=mas[j-1]; mas[j-1]=t; } }
int main() { clrscr(); FILE *filePointer=fopen("massiv.txt","r"); int i=0; while (!feof(filePointer)) { fscanf(filePointer,"%d",&mas[i]); i++; } n=i; puzirek(); for(i=0;i<n;i++) printf("%d ",mas[i]); //scanf("%d",&n); getch(); return 0; }
Программа 6. Пузырьковая сортировка и сортировка методом прямого выбора.
{Сортировка. Алгоритм реализован на языке программирования Turbo-Pascal} uses crt; var M, N : array[0..10] of integer; i:integer;
procedure Input; begin for i := 0 to 10 do begin writeln('Число'); readln(M[i]); {Ввод массива} end; end;
Procedure Sort1; {Пузырьковый метод сортировки} var q,i,x:integer; begin
for i:=10 downto 0 do begin for q:=0 to 10 do if M[q]<M[q+1] then begin x:=M[q]; M[q]:=M[q+1]; M[q+1]:=x end; end; end;
procedure Sort2; {Метод прямого выбора} var i,j,k,x:integer; begin for i:=0 to 9 do begin k:=i; x:=M[i]; for j:=i+1 to 10 do if M[j] >x then begin k:=j; x:=M[k]; end; M[k]:= M[i]; M[i]:=x; end; end;
{---------------------------------------------} begin clrscr; input; {Ввод исходного массива} writeln('Исходный массив'); for i:=0 to 10 do write(M[i],' '); {Вывод исходного массива} writeln; Sort1;{Сортировка массива методом пузырька} writeln ('Сортированный массив'); for i:=0 to 10 do write(M[i],' '); {Вывод отсортированного массива} input; {Ввод исходного массива} writeln('Исходный массив'); for i:=0 to 10 do write(M[i],' '); {Вывод исходного массива} writeln;
sort2; writeln ('Сортированный массив методом прямого выбора'); for i:=0 to 10 do write(M[i],' '); {Вывод отсортированного массива} readln; end.
Программа 7. Сестры.
//Две строки матрицы назовем сестрами, если совпадают //множества чисел, встречающихся в этих строках. Программа //определяет всех сестер матрицы, если они есть, //и выводит номера строк.
Алгоритм реализован на Turbo C++. //#include <graphics.h> #include <stdlib.h> //#include <string.h> #include <stdio.h> #include <conio.h> //#include <math.h> #include <dos.h> #include <values.h> #include <iostream.h>
const n=4,//кол-во строк m=4; //столбцов
int m1[n][m]; //исходный массив struct mas{int i,i1;}; //i-индекс сравниваемой строки с i1 строкой mas a[n*2]; // массив типа mas, где будут лежать сестры, пример) a[1].i и a[1].i1 - сестры
void main() {clrscr(); int i,j; randomize(); for( i=0;i<n;i++) for( j=0;j<m;j++) m1[i][j]=random(2); //случайным образом в массив заносим цифры
for(i=0;i<n;i++) {printf("\n %d) ",i); for(int j=0;j<m;j++) printf(" %d",m1[i][j]); //распечатываем этот массив } int min, p; //индекс минимального элемента после s-го элемента i-ой строки //сортировка строк массива по возрастанию for(i=0;i<n;i++)//i-сортировка i-ой строки { for(int s=0;s<m-1;s++) {min=m1[i][s+1]; for(int j=s;j<m;j++) if(m1[i][j]<=min){min=m1[i][j];p=j;} //запоминаем минимальный элемент в ряде после s-го элемента if(m1[i][s]>=min) {m1[i][p]=m1[i][s];m1[i][s]=min;} //меняем местами s-й и p-й элемент,если s-й>p-го(минимального) }
}
printf("\n"); for(i=0;i<n;i++) {printf("\n %d) ",i); for(int j=0;j<m;j++) printf(" %d",m1[i][j]); //выводим отсортированный массив } int s=0 //сколько элементов в i-й строке совпадают с эл-ми i1 строки, k=0; //сколько строк совпали int i1; for(i=0;i<n-1;i++) //верхняя строка i for( i1=i+1;i1<n;i1++) //нижняя строка i1 {s=0; for(int j=0;j<m;j++) //сравнение идет по j-му столбцу // ! ! if(m1[i][j]==m1[i1][j])s++; //если соответствующие элементы в //i-й и i1-й строки совпадают, то кол-во совпавших увеличивается на 1 if(s==m){a[k].i=i;a[k].i1=i1;k++;} //если все элементы i-й и i1-й строки совпали, то они сестры }
printf("\nСестры :"); for(i=0;i<k;i++) printf("\n %d и %d",a[i].i,a[i].i1); //распечатываем a[i].i-ю и a[i].i1-ю сестру getch(); }
Программа 8. Поиск узоров из простых чисел.
//Построить матрицу А(15 Х 15)таким образом: А(8,8)=1, затем //по спирали против часовой стрелки, //увеличивая значение очередного элемента на единицу //и выделяя все простые числа красным цветом, заполнить матрицу //Алгоритм реализован на Turbo C++.
#include <stdio.h> #include <conio.h>
void main(void) { clrscr(); int mas[15][15]; int n=1,x=6,y=6,k=1; int i,j; while(1){ mas[x][y]=k++; switch(n){ case 1: x++;break; case 2: y--;break; case 3: x--;break; case 4: y++;break; } if(x==15) break;
if(x==y && x<6) n=4; else if(x+y==12 && x<6) n=1; else if(x+y==12 && x>6) n=3; else if(x==y+1 && x>6) n=2;
}
for(i=0;i<15;i++) { for(j=0;j<15;j++) { textcolor(12); if(mas[j][i]>2) for(k=2;k<mas[j][i];k++) if(mas[j][i]%k==0) textcolor(15); cprintf("%3d ",mas[j][i]); } printf("\n"); }
getch(); }
Программа 9. Сортировка строк матрицы.
//Cортировка строк матрицы. В каждой строке подсчитывается сумма //простых чисел. Полученный вектор упорядочивается по возрастанию. //Строки матрицы переставляются по новому вектору. //Алгоритм реализован на Turbo C++. #include<stdio.h> #include<conio.h>
#define n 5
struct summa { int value; int idx; } sum,massum[n],a;
void main(void){ clrscr(); int mas1[n][n],mas[n][n]={{1,1,1,1,1}, {3,16,11,6,4}, {8,10,15,23,1}, {3,8,10,15,3}, {7,3,20,15,10}};
int i,j,k,flag;
for(i=0;i<n;i++){ sum.value=0; for(j=0;j<n;j++){ flag=0; if(mas[i][j]>2) for(k=2;k<mas[i][j];k++) if(mas[i][j]%k==0) flag=1; if(flag==0) sum.value=sum.value+mas[i][j]; } sum.idx=i; massum[i]=sum; }
for(i=0;i<n-1;i++) for(j=0;j<n-1-i;j++){ if (massum[j].value>massum[j+1].value){ a=massum[j]; massum[j]=massum[j+1]; massum[j+1]=a; } }
for(i=0;i<n;i++) for(j=0;j<n;j++) mas1[i][j]=mas[massum[i].idx][j];
for(i=0;i<n;i++){ for(j=0;j<n;j++) printf("%3d ",mas[i][j]); printf("\n"); }
printf("\n\n\n");
for(i=0;i<n;i++){ for(j=0;j<n;j++) printf("%3d ",mas1[i][j]); printf("\n"); } getch(); }
Задача о назначениях (задачи выбора)
Эта задача состоит в следующем. Пусть имеется






Иначе говоря, решение этой задачи представляет собой перестановку (



(

 |
(17.1) |
по всем перестановкам (

Перед нами типичная экстремальная комбинаторная задача. Ее решение путем прямого перебора, то есть вычисления значений функции 17.1 на всех перестановках и сравнения, практически невозможно при сколько-нибудь больших


Конечное множество, на котором задана целевая функция 17.1, представляет собой множество всех перестановок чисел







Элементы матрицы должны быть подчинены двум условиям:
 |
(17.3) |
 |
(17.4) |
Условия 17.3 и 17.4 говорят о том, что в каждой строке и в каждом столбце матрицы

Теперь задача заключается в нахождении чисел

 |
(17.5) |
Казалось бы, что к полученной задаче методы линейного программирования непосредственно применить нельзя, ибо в силу условий 17.2 она формально является целочисленной.
Заменим условие 17.2 на условие неотрицательности переменных
 | (17.6) |
Тем самым мы получаем обычную задачу линейного программирования. В нашем случае требование целочисленности 17.2 будет выполняться автоматически.
Программа 10.Назначение на работу.
program one;{Назначение на работу. Рассматривается случай: 10 работ и 10 желающих. реализовано на Turbo-Pascal} uses crt; const n=10; var C : array [1..n,1..n] of integer; T : array [1..n] of integer; M : array [1..n,1..4] of integer; Sum,tmj,z,min,i,j,tmp:integer;
begin clrscr; randomize; write('work - '); for i:=1 to n do write(i:2,' '); for i:=1 to n do begin writeln; write(i:2,' man '); for j:=1 to n do begin C[i,j]:=random(100); {if M[i,j]>max then max:=M[i,j];} {if C[i,j]<min then begin M[1]:=C[i,j]; M[2]:=i; M[3]:=j; end; } write(C[i,j]:2,' ');
end; end; writeln;
for j:=1 to n do T[j]:=0; Sum:=0; for i:=1 to n do begin writeln; write(i:2,' man '); min:=100; for j:=1 to n do begin if (C[i,j]<min) and (T[j]=0) then begin min:=C[i,j]; M[i,1]:=i; M[i,2]:=j; M[i,3]:=C[i,j]; tmj:=j;
end;
write(C[i,j]:2,' '); end; T[tmj]:=1; {M[i,3]:=min;} Sum:=Sum+M[i,3]; write('=',M[i,3]:2,' man=',M[i,1],' job=',M[i,2]); end; writeln; {for i:=1 to n do begin for j:=1 to n do begin if (i<>j) and (M[i,2]=M[j,2]) then begin M[j,3]:=C[j,1]; for z:=1 to n do begin if (M[j,3]>C[j,z]) and (z<>M[j,2]) then begin M[j,3]:=C[j,z]; M[j,2]:=z; end; end; end; end; writeln('=',M[i,3]:2,' man=',M[i,1],' job=',M[i,2]); end; } write('sum=',Sum); readln; end.
Программа 11.Назначение на работу.
/* Назначение на работу. Рассматривается случай: 6 работ и 6 желающих. */
//Назначение на работу. Реализовано на Turbo C++. #include <stdio.h> #include <iostream.h> #include <stdlib.h> #include <conio.h> #define k 6 int Sum,tmj,i,j,zj,min,tmp,min2,tmj2,p,q,ki; int M[k][4], C[k][k], T[k][2], Temper[k][2]; char a; /*struct myst {int cel; float rac; }; myst ctpyk[k];*/ main() {
Sum=0; min=100; for(i=1;i<k;i++) { T[i][1]=0; printf("\n"); for(j=1;j<k;j++) {C[i][j]=rand()/1000 +1; // printf(" %d ", C[i][j]); } }
for(i=1;i<k;i++) { min=100; printf("\n"); for(j=1;j<k;j++) {
if(C[i][j]<min/* && T[j][1]==0*/) { if(T[j][1]==0) {
min=C[i][j]; //m[i][1] - 4el, m[i][2] -job, m[i][3] - stoimost. M[i][1]=i; M[i][2]=j; M[i][3]=C[i][j]; tmj=j; } /* else { if(C[i][j]<C[T[j][2]][j]) { ki=T[j][2]; T[j][2]=0; // T[j][1]=0; min=C[i][j]; M[i][1]=i; M[i][2]=j; M[i][3]=C[i][j]; tmj=j; for(zj=1;zj<k;zj++) { min2=100; if(C[ki][zj]<min2 && zj!=tmj && T[zj][1]==0) { min2=C[ki][zj]; tmj2=zj; M[ki][1]=ki; M[ki][2]=zj; M[ki][3]=C[ki][zj]; }
} T[tmj2][2]=ki; T[tmj2][1]=min2; }
*/
}
printf(" %d ", C[i][j]); }
T[tmj][2]=i; T[tmj][1]=min; // na4alo mega funkcii /* if(C[i][j]<min && T[j][1]!=0) { for(p=1;pk;p++) { if(C[T[tmj][2]][p] }
} */ //konec.
Sum=Sum+M[i][3]; printf(" $= %d, man= %d, job= %d ",M[i][3],M[i][1],M[i][2]);
}
/* for(i=0;i<k;i++) {ctpyk[i].cel=rand(); ctpyk[i].rac=rand()/1000; printf("%d %f \n", ctpyk[i].cel, ctpyk[i].rac);}
*/ scanf("%d",a); return 0; }
Задача о восьми ферзях
Условие задачи. Найти все такие расстановки восьми ферзей на шахматной доске, при которых ферзи не бьют друг друга.
Анализ задачи. Пусть






С помощью процедуры из пункта 3 будем генерировать по очереди все элементы из




Заметим теперь, что ферзи, которые не бьют друг друга, должны располагаться на разных горизонталях. Поэтому можно упорядочить ферзи и всегда ставить




Программа 4. Расстановка восьми ферзей на шахматной доске.
{ Программа выдает все комбинации ферзей, которые не бьют друг друга. Алгоритм реализован на языке программирования Turbo-Pascal } program ferz; uses crt; const desksize=8; type sizeint=1..desksize; unuses=set of sizeint; combinates=array[shortint] of sizeint; var num:byte; combinate:combinates; unuse:unuses;
function attack(combinate:combinates):boolean; var i,j:byte; rightdiag,leftdiag:combinates; begin attack:=false; for i:=1 to desksize do begin leftdiag[i]:=i+combinate[i]; rightdiag[i]:=i-combinate[i]; end; for j:=1 to desksize do for i:=1 to desksize do begin if (i<>j) and ((leftdiag[i]=leftdiag[j])or(rightdiag[i]=rightdiag[j])) then begin attack:=true; exit; end; end; end;
procedure output(combinate:combinates); var i,j:byte; begin
for i:=1 to desksize do for j:=1 to desksize do begin gotoxy(i,j); if(combinate[i]=j) then write(#2) else write(' '); end; readln; end;
procedure create(num:byte; unuse:unuses; combinate:combinates); var i:byte; begin if num<=desksize then for i:=1 to desksize do begin if i in unuse then begin combinate[num]:=i; create(num+1,unuse-[i],combinate); end; end else if not attack(combinate) then output(combinate);
end;
begin textmode(c40);
clrscr; unuse:=[1..desksize]; create(1,unuse,combinate); end.